Definitionsbereich: Alle Zahlen, die zum Definitionsbereich gehören, heißen Argumente.
Wertebereich: Alle Zahlen, die zum Wertebereich gehören, heißen Funktionswerte.
Als Abszissen-Achse wird die x-Achse und als Ordinaten-Achse die y-Achse bezeichnet.
Nullstellen :Eine Zahl aus dem Definitionsbereich einer Funktion, der bei dieser Funktion die Zahl Null zugeordnet wird, heißt Nullstelle dieser Funktion.
Die Nullstellen einer Funktion sind die Abszissen derjenigen Punkte, in denen das Funktionsbild die x-Achse schneidet bzw. berührt.

Monotonie: Eine Funktion ist monoton fallend, wenn für wachsende Argumente eines Intervalls die zugehörigen Funktionswerte fallen.
Eine Funktion ist monoton steigend, wenn für wachsende Argumente eines Intervalls die zugehörigen Funktionswerte steigen.
Besitzt eine Funktion in einem Intervall einen größten oder kleinsten Funktionswert, so heißt der zugehörige Punkt Extrempunkt (Maximum/Minimum)
Unstetigkeitsstellen:
Nähert sich der Graph immer mehr einer bestimmten Geraden (z.B. x-Achse siehe Abbildung y = 1/x) an, ohne sie jedoch zu erreichen, nennt man diese Gerade Asymptote .
Ist eine Funktion an einer Stelle nicht definiert (z.B. y-Achse Abbildung y=1/x), so heißt dieser x-Wert Polstelle.
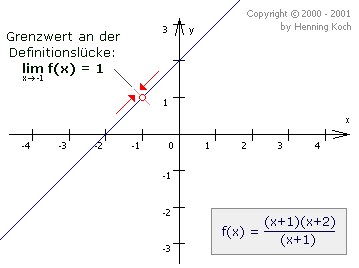
Lücke: linksseitiger Grenzwert=rechtsseitiger Grenzwert und xo gehört nicht zum Definitionsbereich von f
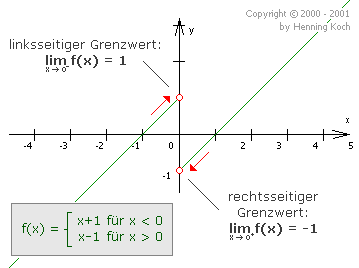
Sprung: rechter Grenzwert entspricht nicht dem linken Grenzwert
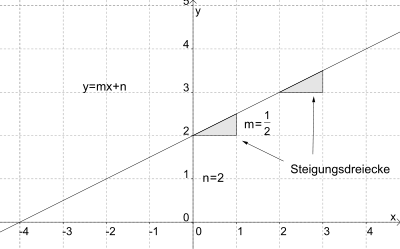
Eine Lineare Funktion besitzt die Form y = mx+n.
Der Graph einer linearen Funktion ist eine Gerade. Der Faktor m ist der Anstieg der Geraden.
n nennt man den Achsenabschnitt. Die Gerade schneidet die y-Achse im Punkt (0;n).
AUFGABE:
Übertrage die Definition von Funktion und die wichtigen Begriffe in dein Lerntagebuch. Gib zu jedem Begriff ein Beispiel an. (Durch Skizzen oder Funktionen).
Eintrag in das Lerntagebuch
|



