|
1.2 Das Tangentenproblem
|

  
|
| Ausgangspunkt für die Definition der Ableitung ist die Näherung der Tangentensteigung
durch eine Sekantensteigung. Gesucht wird ja die Steigung einer Funktion (darstellbar als Graph)
in einem bestimmten Punkt (x0|f(x0).
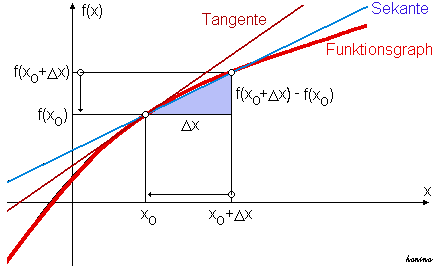
Daher wird zuerst die Steigung der Sekante in einem endlichen Intervall berechnet.

Die Sekantensteigung ist also der Quotient zweier Differenzen; daher auch ihre Bezeichnung "Differenzenquotient". Mit der Kurznotation ∆y für f(x0+∆x)-f(x0) kann
man auch abgekürzt schreiben:
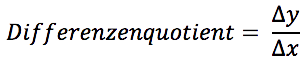
Um nun die Tangentensteigung zu berechnen, muss der Punkt Q dem Punkt P immer weiter
angenähert werden. Das heißt mein ∆x nähert sich Null. Auf diesem
Grenzübergang beruht auch die folgende Definition:
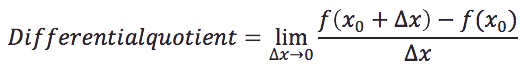
Folgende Animation wird dir diesen Grenzübergang nochmals genauer veranschaulichen.
Lernstoff; Veranschaulichung
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



