|
2.1 Was ist der Differentialquotient?
|
 
|
Der Differentialquotient (auch Ableitung einer Funktion genannt) entspricht der Steigung der Tangente in einem Punkt. Man spricht auch von der "momentanen Änderungsrate".
Lernstoff
|
|
2.3 Beispiele zum Differentialquotient
|
|
Um zu den Beispielen im Worddokument zu kommen, klicke hier. 
Selfchecking Übung, Eintrag in das Lerntagebuch
|
|
2.4 Die Ableitungsregeln
|
|
Mit den folgenden Regeln kann man zusammengesetzte Funktionen ableiten. Achtung: Die Funktionen f,g und h müssen differenzierbar
und reell sein, a ist eine Konstante.
Konstante Funktion: (a)' = 0
z.B. f(x) = 3 Þ f'(x)= 0.
Potenzregel: (xn)' = n·xn-1
z.B.: f(x) = x³ Þ f'(x) = 3x²
Faktorregel: (a·f)'(x)= a·f'(x)
z.B.: f(x)= 3x² Þ f'(x)= 3·2x
Summenregel: (g ± f)'(x)= g'(x) ± f'(x)
z.B.: f(x)= 5x² + 6x³ Þ f'(x)= 10x + 18x²
Produktregel: (g·f)'(x)= g'(x)·f(x) + g(x)·f'(x)
z.B.: f(x)= 3x²·cos(x) Þ f'(x)=6x·cos(x) + 3x²·(-sin(x))
Quotientenregel:
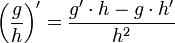z.B.:  Þ 
Kettenregel: (g o f)'(x) = (g(f(x)))' = g'(f(x))·f'(x)
z.B.: f(x)= cos(3x²) Þ f'(x) = -sin(3x²)·6x
...weiter Ableitungsregeln (zu sin, cos, ...) findest du unter
http://www.mathe-online.at/mathint/diff1/i_ableitungen.html. Dort befindet sich auch ein Ableitungsrechner zur Überprüfung!
Lernstoff
|
|
2.5 Übungen zu den Ableitungsregeln
|
|
Hier
findest du die Übungen zu den Ableitungsregeln.
Trage die Übungen in dein Hausübungsheft ein!
Übungsaufgaben, Eintrag in das Hausübungsheft
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|
