Wir wollen uns dem Begriff der Winkelfunktion von zwei Ansätzen aus nähern,
zunächst definieren wir uns Sinus, Cosinus und Tangesn strikt geometrisch am
rechtwinkligen Dreieck:
1. Definition am rechtwinkligen Dreieck
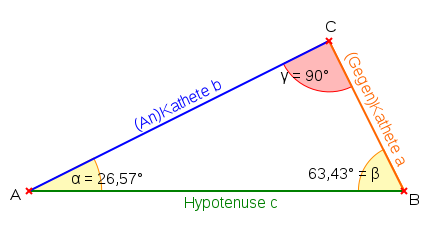
Die Längenverhältnisse der drei Seiten im rechtwinkligen Dreieck sind nur
abhängig vom Maß der beiden spitzen Winkel. Da aber das Maß eines dieser
Winkel über die Winkelsumme den anderen Winkels bereits festlegt,
hängen die Längenverhältnisse im rechtwinkligen Dreieck somit nurnoch vom
Maß eines der beiden spitzen Winkel ab.
Deshalb definiert man die Längenverhältnisse in Abhängigkeit eines der beiden spitzen Winkel:
Sinus
Der Sinus eines Winkels ist das Verhältnis der Länge der Gegenkathete zur Länge der Hypotenuse.
sin(α) = Gegenkathete / Hypothenuse
Cosinus
Der Kosinus ist das Verhältnis der Länge der Ankathete zur Länge der Hypotenuse.
cos(α) = Ankathete / Hypothenuse
Tangens
Den Tangens definieren wir uns als Verhältniss von Sinus zu Cosinus eines Winkels:
tan(α) = sin(α) / cos(α)
Merke
Da Hypotenuse die längste Seite des rechtwinkligen Dreiecks ist (sie liegt per Definition dem größten, also dem rechten Winkel, gegenüber), gilt auch stets:
sin(α) <= 1 und cos(α) <= 1
2. Definition am Einheitskreis
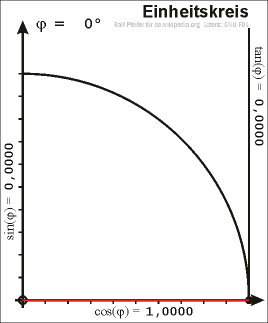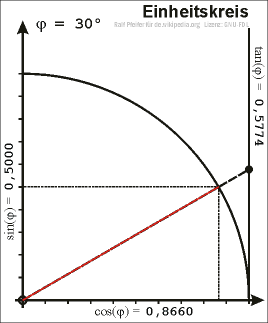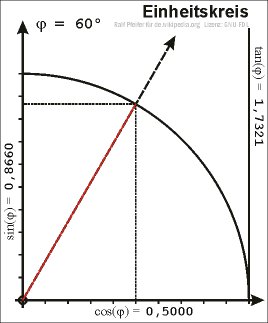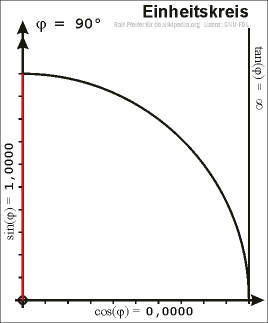Da im rechtwinkeligen Dreieck der Winkel zwischen Hypotenuse und Kathete nur Werte von 0 bis 90 Grad annehmen kann, sind Sinus und Cosinus zunächst nur für solche Winkel definiert.
Um zu einer allgemeineren Definition zu gelangen betrachten wir einen Punkt P mit den Koordinaten (x,y) auf dem Einheitskreis (x²+y²=1). Der Ortsvektor von P schließt mit der x-Achse
einen Winkel α ein. Der Koordinatenursprung (0,0), der Punkt (x,0) auf der x-Achse und der Punkt P(x,y) bilden ein rechtwinkliges Dreieck. Die Länge der Hypotenuse beträgt nun squr(x²+y²)=1, sie entspricht also dem Radius des Einheitskreises.
Die Ankathete des Winkels α ist die Strecke zwischen (0,0) und (x,0) und hat die Länge x, es gilt also:
cos(α) = x
Die Gegenkathete des Winkels α ist die Strecke zwischen (x,0) und(x,y), und hat die Länge y, es gilt also:
sin(α) = y
Die y-Koordinate eines Punktes im ersten Quadranten des Einheitskreises entspricht also dem Sinus des Winkels zwischen seinem Ortsvektor und der x-Achse, die x-Koordinate dem Kosinus des Winkels.
Setzt man jenen Gedanken nun etsprechend für die anderen Quadranten des Einheitskreises geometrisch fort, erhält man eine Definition für Sinus udn Cosinus über die vollen 360°.
Lernstoff
|
