| Dieser Lernpfad dient als Unterlage zu einer Einheit im Hörsaal zum Thema "Funktionen" im Rahmen der Workshops für Analysis im WS 2004/05 an der Universität Wien. |
|  |
|
Hilfe |
|
2. Exakte Definition einer Funktion
|

 
|
Nachdem du nun schon eine Ahnung davon hast, worum es sich um Funktionen handelt, folgt hier eine mathematisch exakte Definition (aus Rindler: "Analysis einer Veränderlichen", Skriptum):

Sprich: "f heißt Funktion von X nach Y, wenn für alle x aus der Menge X gilt: es existiert genau ein y aus der Menge Y mit y entspricht dem Funktionswert von x."
- X ist die Definitionsmenge, das heißt: Man darf für x alle Werte aus der Menge X einsetzen. Fällt dir dazu ein Beispiel ein? Was könnte ein möglicher Definitionsbereich der Funktion f(x)=1/x sein?
Hier steht die Lösung der Frage.
- Y heißt die Zielmenge, das heißt welche Werte können angenommen werden.
- Im(f) heißt Image oder Bildbereich der Funktion. Mathematisch wird das auch so formuliert:
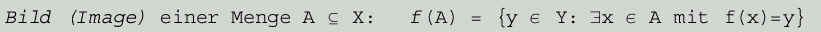
Umgangssprachlich bedeutet das: Unter Bildmenge versteht man alle y aus der Wertemenge, die Funktionswert von einem x aus der Menge A sind.
- Um die Sache noch zu verkomplizieren, gibt es auch noch den Begriff des Urbilds:
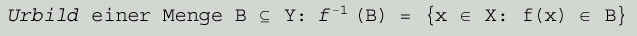
Ausgehend von einer beliebigen Teilmenge B der Wertmenge Y sind das alle jene x, deren Bilder die Elemente aus B sind.
Hier kannst du diese Begriffe noch üben!
Als Graph bezeichnet man die Kombination von allen x und y, die laut Funktion zusammengehören. Das muss also nicht unbedingt eine Zeichnung sein, sondern ist nur eine Menge!
|
|
3. Injektiv, surjektiv, bijektiv
|

 
|
Lies dir die Beschreibung der Begriffe injektiv, surjektiv und bijektiv unter folgendem Link durch und klick auch rechts auf die Beispiele:
Injektiv, surjektiv und bijektiv
|
Lernpfad als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



