|
|
|
|
|
|
|
|
| |
| |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Einführendes Beispiel: Betrachten wir einen Würfel. Ein Würfel hat 6 Seiten, würfelt man mit diesem Würfel so gibt es 6 Möglichkeiten:
Was man aber mit Sicherheit vorraussagen kann, ist die Ergebnissmenge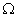 
des Experiments, d.h.: die Menge aller bei diesem
Versuch möglichen Ergebnisse.Beim Würfeln eines Würfels ist dies 
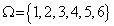
Beim Werfen einer Münze: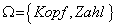 
Nun genügt die Angabe von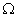
natürlich nicht zur vollständigen Beschreibung eines
Zufallsexperiments.Zusätzlich muss man wissen mit welcher Wahrscheinlichkeit die einzelnen Versuchseergebnisse eintreten. Beim Werfen einer idealen Münze folgt aus Symmetriegründen, daß beide Seiten mit der gleichen Wahrscheinlichkeit auftreten. Da nur 2 Fälle möglich sind gilt: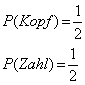 
Beim Würfel ist ebenfalls das Würfeln jeder einzelnen Zahl gleich wahrscheinlich: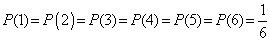 
Betrachtet man einen Reißnagel, so ist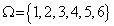
= ( Spitze nach oben, Spitze nach unten)dennoch handelt es sich hier nicht um ein Laplace Experiment, da mangels geeignete Symmetrie, die beiden Ereignisse unterschiedliche Wahrscheinlichkeiten haben. Wir bezeichnen im Folgenden jede Teilmenge von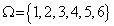
als Ereigniss.Betrachten wir beim Würfeln mit einem Würfel das Ereignis G:"es wird eine gerade Zahl gewürfelt" G = ( 2, 4, 6 )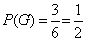 
Das bedeutet, dass die Wahrscheinlichkeit beim einmaligen Würfeln mit einem Würfel eine gerade Zahl zu würfeln bei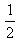 
liegt.
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Das Ziehen geordneter Stichproben mit zurücklegen soll am Beispiel des Urnenmodells veranschaulicht werden. In der Urne befinden sich 2 Kugeln: eine rote und eine blaue Kugel Wie groß ist die Wahrscheinlichkeit 2 mal hintereinander eine blaue Kugel zu ziehen? GRAFIK: 
Es gibt 4 Möglichkeiten: 1) man zieht 2 mal blau 2) man zieht zuerst blau dann rot 3) man zieht zuerst rot dann blau 4) man zieht 2 mal rot Für uns günstig ist jedoch nur die erste der 4 Möglichkeiten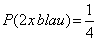 
Berechnet man es nach der Pfadregel so ergibt sich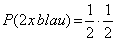 
dies ist die Wahrscheinlichkeit beim 1. Zug eine blaue Kugel zu ziehen mal der Wahrscheinlichkeit beim 2. Zug eine blaue zu ziehen. 
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Hier beschäftigt man sich mit ungeordneten Stichproben. Betrachtet man das oben dargestellt Baumdiagramm und möchte man die Wahrscheinlichkeit berechnen, dass bei 2 Zügen 1 blaue Kugel und 1 rote Kugel gezogen wird, so gibt es 2 Möglichkeiten: 1) es wird zuerst eine rote, dann eine blaue Kugel gezogen 2) es wird zuerst eine blaue, dann eine rote Kugel gezogen Um diese Wahrscheinlichkeit zu berechnen müssen 2 Pfade zusammengefasst werden.
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Zufallsvariable
Eine Zufallsvariable (engl.: random varable)
ist die Zuordnung von Ereignissen eines "Zufallsexperiments"
zu Zahlen. Auf diese Weise ist es möglich, die sprachlich beschreibenen
Ereignisse des Experiments mit den Hilfsmitteln der Mathmatik zu
modellieren. Die einzelnen Werte einer Zufallsvariablen bezeichnet
man als Realisationen, die Menge aller Realisationen als
Definitionsbereich.
Beispiel: Wenn man zwei Münzen auf den Boden wirft, können beide,
eine oder gar kein der beiden Münzen ein Wappen zeigen. Für dieses Zufallsexperiment
lässt sich die Zufallsvariable "Anzahl Wappen" definieren, die dementsprechend
die Realisationen 2, 1 und 0 aufweist. Der Definitionsbereich der Zufallsvariablen
reicht von 0 bis 2, wobei nur ie ganzzahligen Werte zugelassen sind (diskrete
Zufallsvariable).
Unterschiede: Man unterscheidet diskrete und kontinuierliche (stetige) Zufallsvariablen. Erstere haben endlich viele oder abzählbar unendlich viele Realisationen. Letztere können innerhalb ihres Definitionsbereiches jeden beliebigen Zahlenwert annehmen (schließen also Dezimalbrüche mit unendlich vielen Nachkommastellen ein - diese wollen wir aber hier nicht betrachten). Notation: Die Zufallsvariable selbst wird mit Großbuchstaben (X, Y, usw.), ihre Realisation wird mit Kleinbuchstaben bezeichnet (x , y , usw.). Auf diese Weise kann man die Wahrscheinlichkeit, dass die Zufallsvariable X eine bestimmte Realisation hat, so ausdrücken: P(X = x), z.B.: P(X = 2). Das würde also im obigen Beispiel bedeuten: Man berechne die Wahrscheinlichkeit dafür, dass 2-mal, also auf beiden Münzen das Wappen erscheint. Halten wir fest: Die Wahrscheinlichkeit, dass die Zufallsvariable X eine bestimmte Realisation hat, drückt man in der folgenden Weise aus: P(X = x). Erwartungswert und Varianz Der Erwartungswert einer Zufallsvariablen E(X) ist
in ebensolcher Weise ein Schätzwert für den Mittelwert
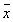wie die Wahrscheinlichkeit ein Schätzwert
für die relative Häufigkei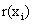t 
ist. Definition: Als Erwartungswert der Zufallsvariablen X bezeichnet man die Zahl E(X):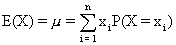 
Die alleinige Angabe des Mittelwertes ist nicht sehr aussagekräftig, weil ja die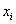 
mehr oder weniger weit von 
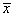abweichen. Der Mittelwert wird daher üblicherweise
samt Streuung angegeben, Analog ist die alleinige Angabe des
Erwartungswertes E(X) = µ nicht sehr aussagekräftig; der Erwartungswert
wird daher üblicherweise ebenfalls samt "Streuung" 
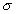angegeben. Diese definiert man als Wurzel aus dem
Erwarungswert de Zufallsvariablen (X - µ)².
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Die Verteilung einer diskreten Zufallsvariablen legt man üblicherweise wie folgt fest:
Würfeln mit einem Würfel. Beschreibe die Verteilung der Zufallsvariaben X sowohl mittels der Wertetabelle als auch mittels des Graphen a) der Wahrscheinlichkeitsfunktion und b) der Verteilungsfunktion! Lösung: a)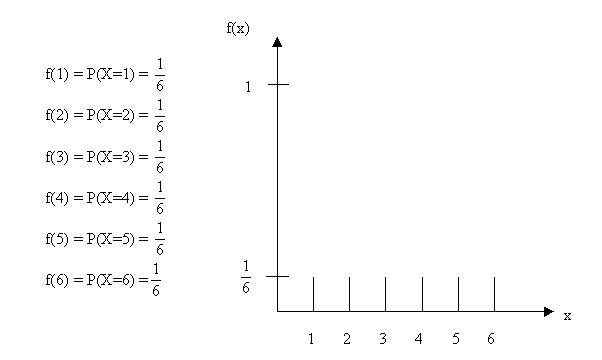 
b) 
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Das Bernoulli-Experiment
Im Gegensatz zu einem Laplace-Experiment, wo alle Ereignisse mit der selben Wahrscheinlichkeit eintreten, fordert ein Bernoulli Experiment zweierlei:
Ein einfaches Bsp. für ein Bernoulli Experiment ist das Ziehen von Kugeln aus einem Glas. Jeder Versuch hat nur zwei Ausgänge und unter der Voraussetzung dass die Kugeln anschließend wieder zurückgelegt werden findet auch jeder Versuch unter den gleichen Bedingungen statt! Betrachten wir ein solches Experiment allgemein: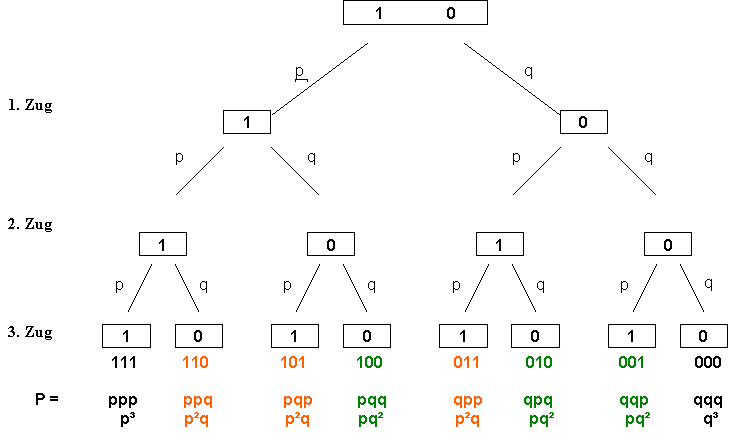 
Daraus folgt: 
Ein konkretes Beispiel: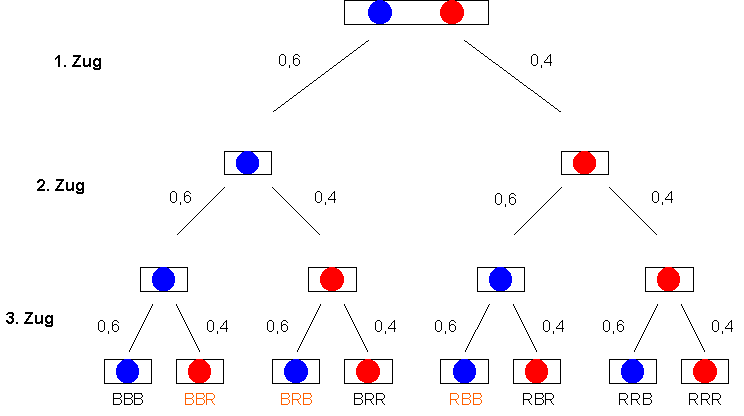 
In unserem Glas befinden sich insgesamt 10 Kugeln, davon 6 Blaue und 4 Rote. Die WK dafür eine blaue Kugel zu ziehen ist also 0,6 die WK für eine rote Kugel ist 0,4. Angenommen wir ziehen 3 mal aus unserem Glas und interessieren uns dafür wie groß die WK ist, dass von diesen 3 Kugeln zwei blaue sind, ist uns die REIHENFOLGE der BEIDEN KUGELN EGAL!! Wichtig ist nur die Anzahl der Erfolge, weil – wie wir gesehen haben – ohnehin alle Erfolge die gleiche WK haben! Wie wir bereits wissen, interessiert man sich bei einem Experiment vielfach nur für die Anzahl X der Erfolge, die bei n Versuchen auftreten, nicht jedoch für die Reihenfolge, in der die Erfolge und Misserfolge eintreten. Unter der Berufung auf den Binomischen Lehrsatz und den Begriff Binomialkoeffizient können wir nun folgendes Gesetz definieren: Verteilungsgesetz Binomialverteilung:
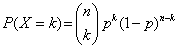
Für unser Beispiel ergibt sich dann: Wahrscheinlichkeit,
dass von 3 gezogenen Kugeln 2 blau sind:
P(X = 2) = P(BBR) + P(BRB) + P(RBB) = 3 * (0,6 * 0,6 * 0,4) = 0,432 = 43,2 %
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
Bei Lotto 6 aus 45 werden aus 45 mit Zahlen
(von 1 bis 45) beschrifteten Kugeln sechs gezogen. Zusätzlich
wird noch eine so genannte Zusatzzahl gezogen. Die Reihenfolge
der gezogenen Zahlen ist dabei aber egal.
Nun wollen wir uns überlegen,
wie groß die Wahrscheinlichkeit für drei
Richtige, vier Richtige, etc. ist, wenn man
pro Runde einen Tipp abgibt.
wobei G für die günstigen und M für die möglichen Ausfälle steht. G und M werden mit dem Binomialkoeffizienten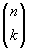 
berechnet,
da es sich, wie schon gesagt, um eine ungeordnete
Stichprobe ohne Zurücklegen handelt.Nun wollen wir uns die möglichen Ausfälle überlegen: Es werden sechs Kugeln gezogen, d.h. k = 6; insgesamt gibt es 45 Kugeln, d.h. n = 45
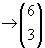
Somit befinden sich die restlichen getippten Zahlen unter den restlichen 39, die
Vier von den getippten Zahlen sind richtig, befinden sich also unter den sechs
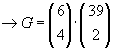
Für die Wahrscheinlichkeit folgt dann:
Um diese Wahrscehinlichkeit zu berechnen,
überlegen wir uns folgendes:
Wir haben ganz sicher einmal fünf Richtige. Das heißt wir überlegen uns nun zuerst die Wahrscheinlichkeit für einen Fünfer mit Hilfe der gerade hergeleiteten Formel:
Nun fehlt noch die Zusatzzahl: a) Zuerst nehmen wir an, dass wir einen Fünfer mit Zusatzzahl haben. Wir betrachten dazu unser Problem als Urnenproblem: Wir haben zu Beginn 45 Kugeln in der Urne: sechs davon sind rot, das sind die sechs getippten Zahlen; der Rest, d.h. 39 Kugeln sind schwarz. Es wurden nun schon sechs Kugeln gezogen, wobei fünf davon rot sind und eine schwarz. Nun befinden sich noch 39 Kugeln in der Urne und zwar 38 schwarze und eine rote. Wenn wir nun fünf Richtige mit Zusatzzahl haben, heißt das, dass die rote Kugel als siebente Kugel gezogen wird. Die Wahrscheinlichkeit, dass die rote
Für unsere Wahrscheinlichkeit heißt das:
b) Nun haben wir einen Fünfer ohne Zusatzzahl. Hier wurde als Zusatzzahl eine der schwarzen Kugeln gezogen.
Mindestens vier Richtige heißt soviel wie entweder vier oder fünf oder sechs Richtige. Darum wird diese Wahrscheinlichkeit aus den einzelnen zusammengesetzt.
Die einzelnen Runden sind voneinander unabhängig, dass heißt die Wahrscheinlichkeiten bleiben immer gleich. Die Zufallsvariable X ist die Anzhal der Sechser in den 104 Spielrunden. Somit ist diese 104-p-binomialverteilt. Da wir mindestens einen Sechser innerhalb des Jahres wollen, suchen wir die
Ein Gewinn heißt soviel wie mindestens drei Richtige.
gearbeitet, wobei
n die Anzahl der Spielrunden
ist. Diese Wahrscheinlichkeit soll nun mindestens 95% betragen.
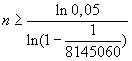
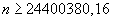
b) Man spielt 100 Spielrunden lang und gibt jeweils 10 Tipps ab. c) Man spielt 10 Spielrunden lang und gibt jewweils 100 Tipps ab. d) Man spielt eine Spielrunde und gibt 1000 Tipps ab. Gibt man in einer Spielrunde mehr als einen Tipp ab, so wird die Wahrscheinlichkeit für einen Tipp mit der Gesamtanzahl der Tipps multipliziert, d.h. wenn man 10 Tipps in einer Runde abgibt, dann ist die Wahrscheinlichkeit für einen Sechser nicht mehr nur 
, sondern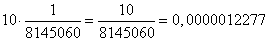 
.
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|
|
|
|
|
|
|
| Zum Seitenanfang Zum Lexikon Zur Galerie Zum Kapitel Wahrscheinlichkeit der Galerie Zum Inhaltsverzeichnis der Mathematischen Hintergründe Zu den Mathe-Links und Online-Werkzeugen Zur Welcome Page |
seines Auftretens an
an, mit der die Zufallsvariable einen Wert 
annimmt. Diese Wahrscheinlichkeiten kann man durch
Aufsummieren der 
bilden: 
,
