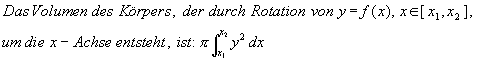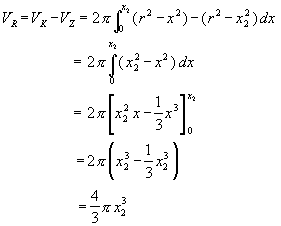Lösung:
Ohne Beschränkung der Allgemeinheit können wir von einem Kreis mit Radius r ³
2 und Mittelpunkt im Ursprung des Koordinatensystems ausgehen. Der Abstand zwischen x1 und x2 beträgt 4 cm (inch).
Der Kreisbogen ist definiert durch ![]() für
für ![]() [ -r, r ], r > 0. Durch Drehung des Kreisbogens im Intervall
[ -r, r ], r > 0. Durch Drehung des Kreisbogens im Intervall ![]() [ x1, x2 ] um die x-Achse entsteht ein
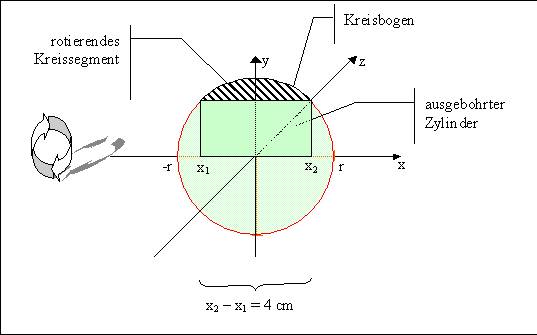
beidseitiger Kugelstumpf. Diesen Kugelstumpf müssen wir uns noch ausgehöhlt denken, d.h. das Volumen des ausgebohrten Zylinders ist vom Volumen des Kugelstumpfs zu subtrahieren.
[ x1, x2 ] um die x-Achse entsteht ein
beidseitiger Kugelstumpf. Diesen Kugelstumpf müssen wir uns noch ausgehöhlt denken, d.h. das Volumen des ausgebohrten Zylinders ist vom Volumen des Kugelstumpfs zu subtrahieren.
Sei VK das Volumen des Kugelstumpfs und sei VZ das Volumen des Zylinders. Gesucht ist das Volumen des sphärischen Rings VR und es gilt VR = VK - V
Z.
Also ist Mit x2 = 2 folgt:
Das Überraschende an diesem Ergebnis: [Folgerung 2]: Das gesuchte Volumen ist gleich dem Volumen einer Kugel mit Anmerkungen und Ergänzungen nehme ich gerne entgegen. |