Kleinere Schriftzeichen   

3 Beispiele für Graphen quadratischer Funktionen:

Für jedes der Beispiele sind drei Arten von Informationen dargestellt: der Graph, die Funktion (Zuordnungsvorschrift) und einige numerische Beobachtungen, die aus den Werten der Koeffizienten folgen, und aus denen die Graphen ermittelt bzw. überprüft werden können. Gehen Sie die Beispiele durch, und überprüfen Sie die numerischen Beobachtungen durch Ablesen am Graphen und durch Rechnung!

Beachten Sie:
    -   Die x-Koordinaten der Schnittpunkte mit der x-Achse sind genau die Nullstellen.
    -   Die y-Koordinate des Schnittpunkts mit der y-Achse ist genau der Funktionswert an der Stelle x = 0.




x ® - (x - 2)2
oder, ausmultipliziert,
x ® - x2 + 4 x - 4

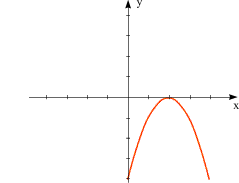
Der Koeffizient von x2 ist -1, also negativ,
daher ist die Parabel nach unten offen.
Schnittpunkt mit der y-Achse bei y = -4
Einzige Nullstelle: x = 2
x ® (x - 2)2 - 1
oder, ausmultipliziert,
x ® x2 - 4 x + 3

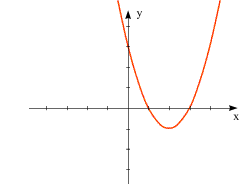
Der Koeffizient von x2 ist 1, also positiv,
daher ist die Parabel nach oben offen.
Schnittpunkt mit der y-Achse bei y = 3
Nullstellen: x = 1 und x = 3
x ® x2/4 - 1



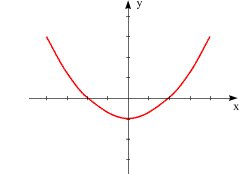
Der Koeffizient von x2 ist 1/4, also positiv,
daher ist die Parabel nach oben offen.
Da 1/4 < 1, ist die Form der Parabel flacher als bei den anderen Beispielen.
Schnittpunkt mit der y-Achse bei y = -1
Nullstellen: x = -2 und x = 2