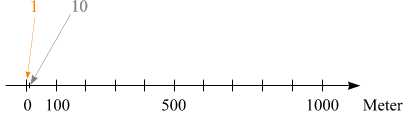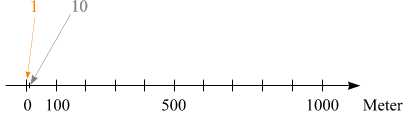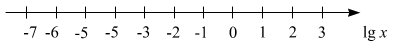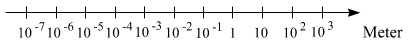Exkurs über die Nützlichkeit des Logarithmus:
Inhalt:
Wir werden uns im Folgenden auf den Zehner-Logarithmus lg beziehen, obwohl
alle Überlegungen auch für Logarithmen zu anderen Basen gelten.
1. Logarithmische Skala
Nehmen wir an, wir wollen die Größenordnungen der auf der Erde lebenden Organismen
auf einer Skala auftragen. Sie soll von der Durchschnittsgröße eines Virus
(etwa ein Zehntausendstel Millimeter, d.h. 10-7 m)
bis zu den größten Pilzgeflechten
(einige Kilometer, d.h. ungefähr 103 m)
reichen.
Die übliche Darstellungsweise von Zahlen auf einer Zahlengeraden,
wie wir sie im Kapitel Zahlen,
kennengelernt haben, würde auf ein Diagramm wie dieses führen:
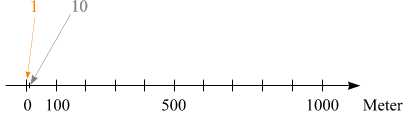
Mit ein bisschen Leben gefüllt, würde es so aussehen:
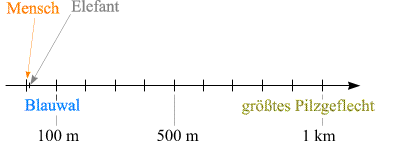
Organismen unterhalb einer Größe von etwa 10 m
finden nur in einem winzigen Intervall Platz, in dem praktisch nichts erkannt werden kann.
Als günstigere Darstellungsweise bietet sich an, anstelle der (in Metern gemessenen)
Größe x der Organismen
deren Logarithmus lg x
zu verwenden, da dieser lediglich den Bereich zwischen -7 und 3
überstreicht:
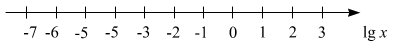
Gleiche Abstände auf dieser Skala entsprechen dem gleichen Faktor
zwischen den Größen. Eine solche logarithmische Skala wird manchmal auch in der Form
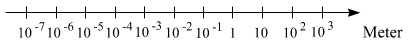
beschriftet, wobei man auch von einem logarithmischen Maßstab spricht.
Beachten Sie, dass der "Nullpunkt", der x = 0
entspricht, nach links "ins Unendliche" gerutscht ist. Nun sieht unsere Galerie
der Organismen schon besser aus:
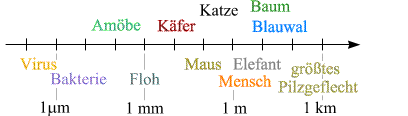
Wir könnten diese Skala auch bequem in beide Richtungen um einige weitere Größenordnungen
erweitern, etwa um auch die allerkleinsten Viren
(10-9 m) unterbringen zu können.
2. Darstellung von Funktionsgraphen und funktionalen Abhängigkeiten
In ähnlicher Weise eignen sich logarithmische Skalen oft dazu, Funktionsgraphen
und funktionale Abhängigkeiten
darzustellen, die sich über einen weiten Bereich von Größenordnungen erstrecken.
Es gibt aber einen weiteren Grund, logarithmische Skalen zu in der Darstellung von Funktionsgraphen zu verwenden:
Ist beispielsweise der Zusammenhang zwischen zwei Größen x
und y durch eine Exponentialfunktion
gegeben, d.h. (unter Verwendung der Basis 10)
y
=
c 10bx,
so ergibt die Anwendung der Funktion lg auf beiden Seiten und die
Ausnutzung der Rechenregeln für den Logarithmus (wir nehmen an, dass
c > 0 ist) die Beziehung
lg y
=
lg c
+ bx.
Wird u = lg y
anstelle von y als
abhängige Größe verwendet, so wird dies zu
u
=
lg c
+ bx,
beschreibt also einen linearen (genauer: linear-inhomogenen) Zusammenhang, dessen Graph eine
Gerade ist! Das ist eine gute Nachricht für alle, die exponentiellen Abhängigkeiten begegnen,
denn Geraden sind einfacher zu zeichnen als die Graphen der Exponentialfunktionen in der üblichen Form.
Wir müssen überdies nicht eigens lg y
als neue Variable u
einführen - es reicht, in der Darstellung
des Graphen auf der y-Achse eine
logarithmische Skala zu verwenden.
Wir können sogar mehr sagen:
y hängt von x
genau dann exponentiell ab (mit positivem c), wenn der Zusammenhang der beiden Größen in einem Diagramm, dessen
y-Achse einen logarithmischen Maßstab
trägt, durch eine Gerade dargestellt wird.
Sehen wir uns anhand eines typischen Beispiels an, wie diese Tatsache zur Erkennung exponentieller Zusammenhänge
verwendet wird. Wir stellen uns vor, eine Menge von Datenpunkten, d.h. von
Paaren (x, y)
zur Verfügung zu haben, für die ein exponentieller Zusammenhang
- mit zunächst unbekannten Parametern
b und c
- vermutet wird. Als erstes werden die Paare
(x, lg y)
in ein Diagramm eingetragen:
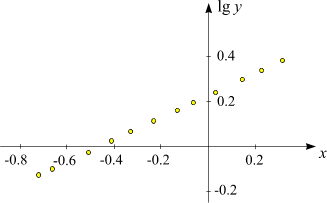
Die Anordnung der Punkte zeigt eine recht gut definierte Gerade, woraus wir
schließen, dass y in guter Näherung
exponentiell von x abhängt.
Wir legen die Gerade durch die Datenpunkte (bzw. ermitteln die "beste" Gerade, die sich
durch die "Datenwolke" legen lässt - mit welchen Mitteln das zu bewerkstelligen ist, muss uns hier nicht
interessieren):
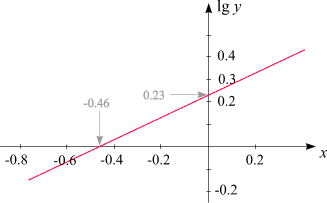
Damit lassen sich die Parameter
b und c
einfach bestimmen:
b ist der Anstieg
der Geraden, lg c
ist der Abschnitt auf der vertikalen Achse. Wir lesen ab:
b = 0.5 und
lg c = 0.23,
woraus c = 100.23 = 1.698... »
1.7 folgt. Auf diese Weise bestimmen wir den gesuchten Zusammenhang
- innerhalb der Ablesegenauigkeit -
als
y
= 1.7 × 10x/2 .
Hätten wir mit einem konventionellen (x-y)-Diagramm
gearbeitet, dann hätte die Anordnung der Datenpunkte so ausgesehen:
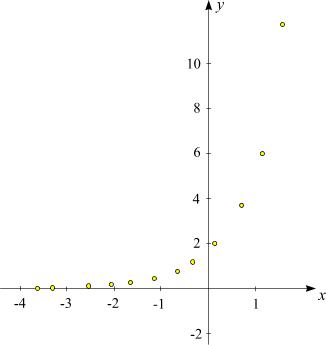
Es wäre wesentlich schwieriger gewesen, auch nur festzustellen, ob der durch sie dargestellte
Zusammenhang in guter Näherung exponentiell ist.
Und selbst wenn es mit einigem Geschick gelänge, den Graphen der Funktion zeichnen,
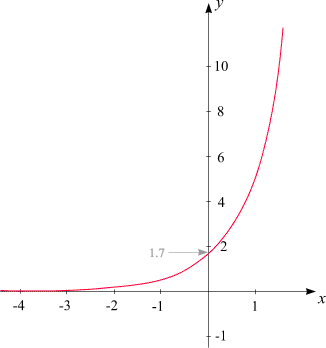
so ließe sich lediglich der Koeffizient c
direkt als 1.7 ablesen, während die Ermittlung
des (Wachstums-)Parameters b, der
für die meisten Zwecke der wichtigere ist, um einiges komplizierter und unverlässlicher
wäre als mit der "logarithmischen Methode".
Ein weiteres Beispiel für die Nützlichkeit logarithmischer Skalen
bildet die Klasse der Potenzfunktionen
y
=
C xn
für positives C.
Die Anwendung der Funktion lg auf beiden Seiten und die
Ausnutzung der Rechenregeln für den Logarithmus führt auf die Beziehung
lg y
=
lg C
+ n
lg x.
Der Graph einer solchen Funktion nimmt in einem Diagramm, in dem beide Achsen einen
logarithmischen Maßstab tragen (einem so genannten "doppelt-logarithmischen Diagramm", in dem
u = lg x
und v = lg y
anstelle von
x und y
verwendet wird),
die Form einer Geraden an, deren Anstieg mit dem Exponenten n
übereinstimmt.
Ebenso wie im vorigen Beispiel wird diese Tatsache dazu benutzt, festzustellen, ob (und mit welcher Güte)
eine gegebene Menge von Datenpunkten eine Potenzfunktion beschreibt, und sie erlaubt die Bestimmung der
Parameter C und n.
Um derartige Methoden bequem anwenden zu können, kann (einfaches und doppeltes) Logarithmenpapier zu Hilfe
genommen werden, d.h. eine Variante des "Millimeterpapiers", in dem für eine oder beide Koordinaten
ein logarithmischer Maßstab verwendet wird. Dank seines feinen logarithmischen Koordinaten-Netzes
können auf ihm Datenpunkte direkt (ohne vorherige Berechnung ihrer Logarithmen) eingetragen werden.
3. Logarithmentafel
Eine der nützlichsten Eigenschaften des Logarithmus
wurde mehrere Jahrhunderte lang dazu benutzt, um numerische Berechnungen zu erleichtern.
Insbesondere erlaubt es die Regel
"Der Logarithmus eine Produkts ist gleich der Summe der Logarithmen",
Multiplikationen auf (leichter auszuführende) Additionen zurückzuführen.
Wir illustrieren das Prinzip anhand der Multiplikation
15.5 × 23.6
Eine Logarithmentafel ist im Grunde genommen nichts anderes als eine
riesige Wertetabelle der Logarithmusfunktion lg.
In unserem Beispiel werden der Tabelle die (gerundeten) Logarithmen der Zahlen 15.5 und 23.6
entnommen und addiert. Das Ergebnis ist 2.56324.
Nun wird jene Zeile der Tabelle gesucht, in der 2.56324 als Logarithmus auftritt.
(Dieser Vorgang wird auch "entlogarithmieren" genannt).
Die Zahl, deren Logarithmus 2.56324 ist, ist das gesuchte Produkt, nämlich die Zahl 365.8:
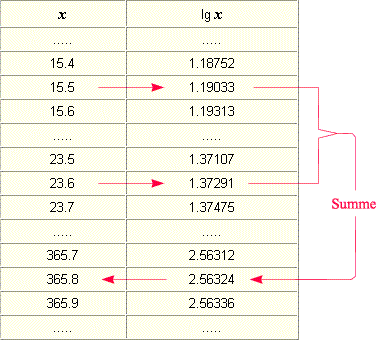
Die nötige Addition 1.19033 + 1.37291 = 2.56324 wird
entweder im Kopf oder auf einem Blatt Papier ausgeführt.
Die Methode lässt sich problemlos auf Produkte mit mehreren Faktoren ausweiten.
In ähnlicher Weise können Divisionen auf Subtraktionen (und Potenzen auf
Multiplikationen) zurückgeführt
werden, und in den historischen Logarithmentafeln wurden auch die Logarithmen spezieller Funktionen wie
Winkelfunktionen (siehe das entsprechende Kapitel)
einbezogen. In den vergangenen Jahrhunderten wurden derartige Tabellen von fleißigen Menschen in
mühevoller Arbeit erstellt. Mit ihrer Hilfe war es auch vor der Entwicklung elektronischer Rechenhilfen möglich,
eine Vielzahl numerischer Berechnungen (mit der Genauigkeit, die die jeweils verwendete
Tafel zuließ) in kurzer Zeit durchzuführen.
Nachbemerkungen:

1. Wir haben das obige Beispiel so gewählt, dass keine Rundungsfehler auftreten.
In der Praxis wird man nicht immer die gewünschte Zahl in der rechten Spalte finden,
sondern mit der ihr am nächsten kommenden Vorlieb nehmen müssen.

2. Tatsächlich ist eine Logaritmentafel nicht so umfangreich, wie es hier aussehen mag:
Ist beispielsweise lg(1.54) bereits als 0.187521 tabelliert, so kann lg(15.4) als
lg(10 × 1.54) = 1+ lg(1.54) = 1.187521
ermittelt werden, muss also nicht eigens in der Liste aufscheinen: Die relevante Information hängt
nur von der Ziffernfolge ab, nicht von der Stellung des Kommas (Dezimalpunkts).
Indem nur ein Größenordnungsbereich (z.B. zwischen 1 und 10) tabelliert wird,
kann die Tabelle kürzer gehalten werden. Die Zehnerpotenz des Resultats
(die Stellung des Dezimalpunkts) wird dann in einem letzten Schritt
eigens ermittelt.
4. Rechenschieber (Rechenstab)
Das Prinzip der Multiplikation, das den Logarithmentafeln zu Grunde liegt, kann
geometrisch gedeutet werden, indem Strecken, deren Längen Längen den Logarithmen der Faktoren entsprechen,
aneinandergelegt werden. Im Rechenschieber (Rechenstab) wird diese Idee durch die Verwendung
zweier verschiebbarer Leisten, auf denen sich logarithmischen Skalen befinden,
realisiert. Das folgende Bild zeigt die Einstellung eines solchen Geräts für die Multiplikation
15.5 × 23.6:

Hier sind die Zahlen, die eingestellt bzw. abgelesen werden, gekennzeichnet:

Sie erkennen, dass eigentlich die Rechnung 1.55 × 2.36 ausgeführt und
das Resultat nur näherungsweise als 3.66 (statt exakt 3.658)
abgelesen werden kann. Die korrekte Stellung des Dezimalpunkts wird zum Schluss bestimmt,
so dass sich
15.5 × 23.6 » 366
ergibt.
Die anderen Skalen, die Sie auf diesen Bildern sehen, betreffen weitere nützliche Dinge,
insbesondere Potenzfunktionen und Winkelfunktionen.
Die Genauigkeit dieses Instruments ist zwar begrenzt, aber als "tragbarer Rechner",
der Multiplikation, Division und einige andere Funktionen "beherrscht",
hat es - bis der Taschenrechner aufkam -
Handwerker, Ingenieure und nicht zuletzt zahlreiche Generationen von SchülerInnen begleitet.