Beweis: Sinus und Cosinus im rechtwinkeligen Dreieck

Beweis...

...der Beziehungen

sin a =

Gegenkathete

Hypotenuse

cos a =

Ankathete

Hypotenuse

im rechtwinkeligen Dreieck:

Gegeben Sei ein rechtwinkeliges Dreieck, dessen Hypotenuse c mit der Kathete b den Winkel a einschließt. b ist dann die Ankathete; die Gegenkathete nennen wir a.

Wir betrachten ein zweites rechtwinkeliges Dreieck, das denselben Winkel a besitzt, dessen Hypotenuse aber die Länge 1 hat. Aufgrund der Definition der Winkelfunktionen haben die Katheten dieses Hilfsdreiecks die Längen sin a und cos a.
Nun legen wir die beiden Dreiecke, wie in der folgenden Skizze gezeigt, übereinander:

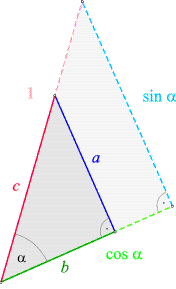
Das ist natürlich deshalb möglich, weil sie den Winkel a gemeinsam haben. Ob das ursprüngliche Dreieck größer oder kleiner als das Hilfsdreieck ist, hängt davon ab, ob c größer oder kleiner als 1 ist. In der obigen Skizze ist c < 1. Das gegebene Dreieck ist mit kräftigen, das Hilfsdreieck mit blassen Farben dargestellt.

Klarerweise sind die beiden Dreiecke zueinander ähnlich. Aufgrund des Strahlensatzes gilt

sin a

und

cos a

was genau die behaupteten Beziehungen sind.

Damit ist auch bewiesen, dass die Verhältnisse a/c und b/c nur vom Winkel a, nicht aber von der Größe des gegebenen Dreiecks abhängen.
Nachbemerkung: Wir sehen anhand dieser Argumentation recht deutlich, dass sin a und cos a als Verkürzungsfaktoren betrachtet werden können: Um diese Faktoren sind die Gegenkathete bzw. die Ankathete kürzer als die Hypotenuse, und sie sind in jedem rechtwinkeligen Dreieck, das den Winkel a besitzt, dieselben.