Beweise: Werte der Winkelfunktionen für spezielle Winkel

Beweise: Werte der Winkelfunktionen für spezielle Winkel:

Die Werte für a = 0°, 90°, 180° und 270° ergeben sich in trivialer Weise aus den Definitionen der Winkelfunktionen bzw. aus den Zeigerdiagrammen.

Beweis für a = 30° und 60°

Diese beiden Winkel treten im gleichseitigen Dreieck auf, wenn zusätzlich eine Höhe eingezeichnet wird:

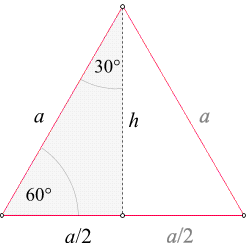
Gemäß dem pythagoräischen Lehrsatz für das hervorgehobene (rechtwinkelige) Dreieck haben wir

a² -

⎛
⎜
⎝

⎞
⎟
⎠

= h²,

d.h.

3 a²

= h²,

woraus

h =

__
Ö 3

folgt. Die Hypotenuse des hervorgehobenen Dreiecks ist a. Für den Winkel 30° ist h die Ankathete und a/2 die Gegenkathete; für den Winkel 60° ist h die Gegenkathete und a/2 die Ankathete. Daraus ergibt sich unmittelbar

sin(30°)

a/2

cos(30°)

__
Ö 3

sin(60°)

__
Ö 3

cos(60°)

a/2

wobei alle Nenner rational gemacht wurden.

Beweis für a = 45°

Dazu betrachten wir ein rechtwinkelig-gleichschenkeliges Dreieck:

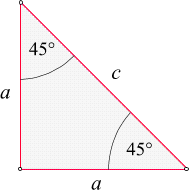
In diesem Fall liefert der pythagoräische Lehrsatz

c   =   a   __
Ö 2

(was nichts anderes als die Formel für die Diagonale des Quadrats ist). Die Hypotenuse des Dreiecks ist c. An- und Gegenkathete für den Winkel 45° sind beide gleich a. Daher ist

sin(45°)    =   cos(45°)    =    1
Ö2
º 1
2
  __
Ö 2

,

wobei im letzten Schritt der Nenner rational gemacht wurde.