Kleinere Schriftzeichen   

Sinus und Cosinus in der Physik - zwei Beispiele:

Die beiden hier vorgestellten Anwendungsbeispiele für Winkelfunktionen in der Physik sollen Sie in erster Linie neugierig machen. Falls Sie den Stoff des Kapitel noch nicht kennen, versuchen Sie dennoch, diese Seite zu lesen, und kommen Sie später wieder hierher zurück!


1. Die Drehbewegung

Betrachten wir ein (kleinen) Körper, der sich auf einer Kreislinie mit Radius r gleichmäßig im Gegenuhrzeigersinn bewegt. Wenn er sich an einer Position befindet, die, wie in der folgenden Skizze dargestellt, durch den Winkel a charakterisiert ist,


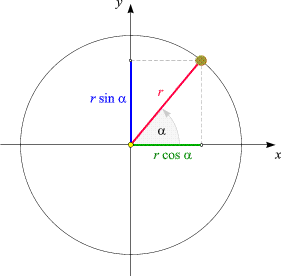
dann sind seine Koordinaten durch

 x  =  r cos a
y  =  r sin a

gegeben. Das ist eine unmittelbare Folge der Definitionen von Sinus und Cosinus.

Während sich der Körper gleichmäßig bewegt, nimmt der Winkel a gleichmäßig mit der Zeit zu: Der überstrichene Winkel a ist zur dafür benötigten Zeit t proportional. Hat die Bewegung zur Zeit t = 0 mit dem Winkel a = 0° (d.h. auf der positiven x-Achse) begonnen, so ist zu einer späteren Zeit t

a  =  w t,

wobei w eine Konstante ist, die Winkelgeschwindigkeit oder Kreisfrequenz heißt. Ist beispielsweise w = 30°/sec, so wird pro Sekunde ein Winkel von 30° überstrichen. Nach 12 Sekunden ist eine volle Umdrehung erreicht, und danach beginnt die nächste Runde. Die Koordinaten des Körpers zur Zeit t sind demnach

x  =  r cos(w t)
y  =  r sin(w t) .

Diese Formeln sind der Ausgangspunkt für das Studium der Drehbewegung. Sie sind nicht auf die Bewegung kleiner Körper auf Kreislinien beschränkt, sondern können auch die Rotation eines starren Körpers um eine fixe Achse beschreiben.


2. Die harmonische Schwingung

Begegnet man schon der Drehbewegung recht häufig in der Physik, so sind Schwingungsvorgänge noch öfter in physikalischen Systemen anzutreffen. Unter allen Arten von Schwingungsvorgängen ist eine besonders wichtig: der Typ der harmonischen Schwingung. Es handelt sich dabei um eine Schwingungsform, die von der Drehbewegung abgeleitet werden kann: Betrachten wir wie oben einen gleichmäßig auf einer Kreislinie bewegten Körper, und lassen wir parallele Lichtstrahlen (horizontal oder vertikal) einfallen. Eine harmonische Schwingung ist ein Bewegungsvorgang von dem Typ, wie ihn der Schatten (die Projektion) des Körpers auf der entsprechende Koordinaten-Achse definiert:


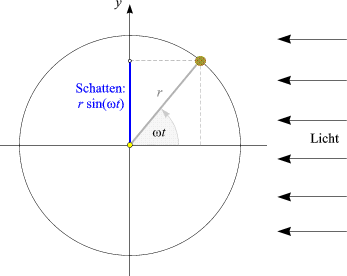
Ganz allgemein spricht man von einer harmonischen Schwingung, wenn sich eine physikalische Größe a in einer derartigen Weise zeitlich verändert. Angesichts unserer obigen Formeln ist eine typische harmonische Schwingung durch

a  =  A sin(w t)

gegeben, wobei (wie vorhin) die Kreisfrequenz w bestimmt, wie schnell der Vorgang abläuft. Die Konstante A stellt den maximalen Wert der Größe a dar (der Sinus kann ja maximal 1 werden) und heißt Amplitude. Falls es sich um die Bewegung des Schattens eines kreisenden Körpers handelt, ist sie gleich dem Radius r des Kreises. Wir könnten statt der Sinus- auch die Cosinusfunktion verwenden oder t durch t - t0 ersetzen (für eine Konstante t0). Beides würde nichts Wesentliches am Typ des Vorgangs ändern, sondern ihn nur zeitlich verschieben. Die letzte Formel macht auch verständlich, warum man von einer Sinus-Schwingung spricht.

Da eine Schwingung die zeitliche Veränderung einer Größe beschreibt, kann man durch die Schreibweise

a(t)  =  A sin(w t)

die Tatsache, dass a von t abhängt, besser zum Ausdruck bringen: die Größe a ist tatsächlich eine Funktion (der Zeit).

Viele Schwingungsvorgänge in der Natur lassen sich (zumindest näherungsweise und für eine gewisse Zeit lang) als harmonische Schwingungen beschreiben. Physikalisch kann es sich bei a beispielsweise um handeln. Diese Liste veranschaulicht, wie universal das Konzept der harmonischen Schwingung ist.