Für die SchülerInnen
der 5a und 5b des BG|BRG Purkersdorf.
Folgende
Eigenschaften von Funktionen sollst du mittels mathe-online
erlernen:
Definitionsbereich, Wertebereich, Nullstellen,
Monotonie und bijektiv. |
|
 | |
Hilfe |
1. Funktionen 1 -
Mathematische Hintergründe
http://www.mathe-online.at/mathint/fun1/i.html
|

     |
Definitionsbereich - Wertebereich
Lies dir
das Kapitel genau durch!
Erkläre (schriftlich) mit eigenen
Worten die Begriffe Definitions- und Wertebereich!
Mithilfe
des folgenden Applets
kannst du etwas über den Definitions- und Wertbereich von Funktionen
herausfinden!
Verschiebe den Wert auf der x-Schiene und beobachte
die Veränderung auf der y-Schiene.
Teste die
Funktionen:
f(x) = 3x + 2; g: x -> x²; h: y = x³ 1
f(x) = --- Wie verhält sich die Funktion an der Stelle Null? Begründe!
x
Besprich deine Ergebnisse mit einem Partner /
einer Partnerin!
Lernstoff
|
2. Funktionen 1 -
Mathematische Hintergründe
http://www.mathe-online.at/mathint/fun1/i.html
|

     |
Nullstellen
Lies dir den kurzen Abschnitt
zur Nullstelle genau durch!
Erkläre (schriftlich) mit eigenen
Worten, was eine Nullstelle ist!
Schau dir nun die folgenden
drei Funktionen an und gib ihre Nullstelle (näherungsweise)
an!
Funktion
Funktion
Funktion
Speichere
die Funktionen in deinem Ordner, drucke sie aus und markiere die
Nullstellen färbig!
Schreib deinen Namen auf die Blätter und
gib sie ab!
Überlege, wie du eine Nullstelle berechnen
kannst!
Schreib deine Vermutung auf und besprich sie mit einem
Partner / einer Partnerin.
Lernstoff
|
| 4. Minimum und
Maximum |

  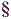 |
Definition:
Der größte Wert der
Wertemenge/des Wertebereichs heißt Maximum.
Der
kleinste Wert der Wertemenge/des Wertebereichs heißt
Minimum.
Hinweis: Verändert man den
Definitionsbereich, dann kann sich auch das Maximum/Minimum
ändern!
MAX/MIN
Drucke
das Beispiel aus!
Übung:
Speichere die Funktion in
deinem Ordner und drucke sie aus!
Gib zu den folgenden
Definitionsbereichen (näherungsweise) Minimum und Maximum der
Funktion an!
Markiere die Bereiche und die Min- und Maxstellen
färbig!
[-2,5 ; -1]
[-1 ; 1]
[1 ; 2,5]
Lernstoff
|
5. Bijektiv
http://www.mathe-online.at/mathint/fun1/i.html#EvF
|

     |
Lies dir
die Erklärungen zu den Begriffen: injektiv, surjektiv und
bijektiv durch.
(Du findest dies am
Kapitelende.)
Schau dir auch die Beispiele an!
Schreib ab,
wann eine Funktion bijektiv ist!
Schreib auch die Definition von
"bijektiv" aus dem Buch (Seite
127) ab!
Lernstoff
|
| 6. Hausübung |

   |
Löse das
Beispiel 333, Buch Seite
130!
Übungsaufgabe
|
Lernpfad als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen
Zugang anlegen. Als registrierter User können Sie
ein persönliches Lerntagebuch
zu diesem Lernpfad anlegen.
|