Exponentielle Wachstums- und Abnahmeprozesse beschreiben ein sich pro Zeiteinheit um einen fixen Prozentsatz ändernden Bestand einer Ausgangsmenge , wobei der jeweils addierte, bzw. subtrahierte Betrag vom Bestand im vorhergehenden Zeitpunkt abhängt.

Durch diese zeitliche Abhängigkeit sind die sich ändernden Beträge im Allgemeinen jedes Mal unterschiedlich, was das exponentielle Wachstum vom linearen Wachstum unterscheidet.

Quelle: http://1.bp.blogspot.com

Weitere Informationen zu exponentiellem Wachstum auf Wikipedia

Um exponentielle Wachstums- und Abnahmeprozesse verstehen zu können, ist es erforderlich, Exponentialfunktionen zu verstehen. Dieses Grundwissen wird in diesem Lernpfad vorausgesetzt.

Man betrachte folgende allgemeine Ausgangssituation:

Es existiert zum Zeitpunkit ein Startkapital, welches wir mit 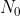bezeichnen und eine jährliche Verzinsungsrate von . Ein Jahr später, zum Zeitpunkt berechnet sich das Gesamtkapital 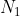mithilfe folgender Gleichung:

Um diese Formel etwas zu vereinfachen, dh. um sich eine Addition zu ersparen, wird ein Wachstumsfaktor eingeführt. Somit ergibt sich folgende Äquivalenz:

Aus der Gleichheit beider Formeln lässt sich somit herleiten:

Zum Zeitpunkt berechnet sich das Gesamtkapital folgendermaßen, wenn wir verwenden:

Im Zeitpunkt :

Betrachtet man nun diese 3 Berechnungen, so lässt sich ein Muster für die Berechnung des Gesamtkapitals in einem beliebigen Zeitpunkt erkennen:

Verwendet man nun diese Rekursionsformel, so erhält man eine allgemeingültige Funktion, mit welcher prinzipiell jeder exponentielle Wachstums- und Abnahmeprozess beschrieben werden kann.

kennzeichnet den Wachstumsfaktor, der je nach seinem Wert einen Wachstums- oder Abnahmeprozess beschreibt. Sei eine Exponentialfunktion der Form: , dann gilt folgende Definition:

Wie bereits in Kapitel 1.2 beschrieben, können Exponentialfunktionen auch als eine Hintereinanderausführung von Multiplikationen betrachtet werden, zB.:

Betrachtet man diese Äquivalenz, so erkennt man, dass man für die selbe Berechnung in dieser Schreibweise Multiplikationen benötigt, wohingegen als Exponentialfunktion nur eine Multiplikation, dafür aber auch eine Exponentation erforderlich ist. Rein rechnerisch besteht hier kein Unterschied in der Ausführung, wohl aber in der Kompaktheit der Aussage. Das Einsetzen in eine Exponentialfunktion stellt sich als wesentlich komfortabler heraus, als in Multiplikationen explizit durchführen zu müssen.

Weitere Informationen zur Exponentialfunktion auf Wikipedia

Um die hergeleitete allgemeine Formel anwenden zu können, ist es erforderlich, auch Elemente abgesehen von zu berechnen. Grundsätzlich gilt: um ein beliebiges Element berechnen zu können, müssen alle anderen Elemente daraus gegeben sein.

Berechnung des Wachstumsfaktors :

Berechnung des Zeitpunktes : (erfordert im allgemeinen Fall eine Basisumrechnung des Logarithmus)

Berechnung der ursprünglichen Menge :

Oft ist es üblich, speziell bei der Beschreibung von Halbwertszeiten, was gleichbedeutend einem exponentiellen Abnahmeprozess ist, eine modifizierte Form der hergeleiteten Formel zu verwenden:

steht für die "Euler'sche Zahl" und für den Wachstumsfaktor. Der Zusammenhang zwischen ausgehend von dieser Darstellung und in der vorhergehenden Formel ist folgender:

Die Funktion (logarithmus naturalis) beschreibt dabei den "natürlichen Logarithmus".

Um nun eine exponentielle Abnahme in dieser Darstellungsform beschreiben zu können, wird die "additive Inverse" von in die Formel eingesetzt. ( statt )

Sei eine Exponentialfunktion, dann gilt folgende Definition: