Klick den oben angezeigten Link an und lies dir die Defintion
der komplexen Zahlen genau durch. Dann klicke auf grafische
Darstellung und lies dir auch diese Seite durch.
Anschließend sollst du folgende Übungsaufgaben machen:
Lückentext zu den komplexen Zahlen
Solltest du die Übung nicht zu 100% geschafft haben lies dir
den Text über Defintion und grafische Darstellung von komplexen
Zahlen noch einmal durch und Versuche die Übung erneut.
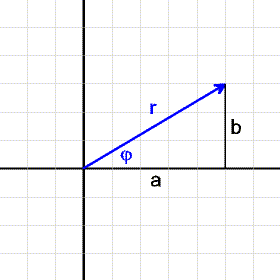 Die komplexen Zahlen können auf zwei verschiedene Arten auf der Gauss'schen Zahlenebene
dargestellt werden. Oben hast du bereits die Normalform kennengelernt.
Die zweite Darstellungsmethode ist die sogenannte Polarform. Für sie müssen wir zuerst noch
neuen Begriff einführen, den Betrag einer komplexen Zahl.Der Betrag einer komplexen
Zahl entspricht der Länge ihres Zeigers in der Gauss'schen Zahlenebene.
In der obigen Abbildung wird er mit r bezeichnet.
Wenn z eine komplexe Zahl ist schreibt man den Betrag
von z als |z|.
Der Betrag einer komplexen Zahl errechnet sich folgendermaßen:
|z|=(a²+b²)^(1/2)
Wobei a der Realteil und b der Imaginärteil von z ist.
Die Polardarstellung von komplexen Zahlen unterscheidet sich
eigentlich nicht von der Polardarstellung von Punkten auf der
Ebene. Sie ist abhängig vom Betrag der komplexen Zahl und dem
Winkel φ, den dieser Betrag mit der reelen Achse einschließt.
Daraus ergibt sich folgende Umrechnung.
Umrechnung von Polarform in Normalform:
a = r·cos φ
b = r·sin φ
Umrechnung von Normalform in polarform:
r=(a²+b²)^(1/2)
φ=arctan(b/a)
Veranschaulichung der beiden Darstellungen
Die komplexen Zahlen können auf zwei verschiedene Arten auf der Gauss'schen Zahlenebene
dargestellt werden. Oben hast du bereits die Normalform kennengelernt.
Die zweite Darstellungsmethode ist die sogenannte Polarform. Für sie müssen wir zuerst noch
neuen Begriff einführen, den Betrag einer komplexen Zahl.Der Betrag einer komplexen
Zahl entspricht der Länge ihres Zeigers in der Gauss'schen Zahlenebene.
In der obigen Abbildung wird er mit r bezeichnet.
Wenn z eine komplexe Zahl ist schreibt man den Betrag
von z als |z|.
Der Betrag einer komplexen Zahl errechnet sich folgendermaßen:
|z|=(a²+b²)^(1/2)
Wobei a der Realteil und b der Imaginärteil von z ist.
Die Polardarstellung von komplexen Zahlen unterscheidet sich
eigentlich nicht von der Polardarstellung von Punkten auf der
Ebene. Sie ist abhängig vom Betrag der komplexen Zahl und dem
Winkel φ, den dieser Betrag mit der reelen Achse einschließt.
Daraus ergibt sich folgende Umrechnung.
Umrechnung von Polarform in Normalform:
a = r·cos φ
b = r·sin φ
Umrechnung von Normalform in polarform:
r=(a²+b²)^(1/2)
φ=arctan(b/a)
Veranschaulichung der beiden Darstellungen
Lernstoff, Übungsaufgabe
|



