|
2.1 Lösen von quadratischen Gleichungen
|

 

|
Mit den komplexen Zahlen ist es nun möglich jede beliebige quadratische Gleichung zu lösen.
Durch die zuvor erworbenen Kenntnisse wird es dir jetzt möglich sein folgende Gleichungen zu lösen.
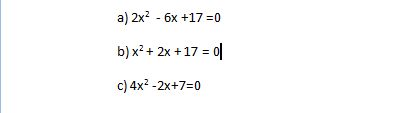
Lösung
Übungsaufgaben
|
|
2.2 Übung zur Darstellung von komplexen Zahlen
|

 

|
Bevor wir nun die Anwendung von komplexen Zahlen in der Physik besprechen,
machen wir noch eine Übung zur Darstellung von komplexen Zahlen.
Gib die in kartesischer Binomialform gegebene Zahl z = 4+3i in Polardarstellung an.
Zeichne dir zuerst eine Skizze, trage den Punkt, der z repräsentiert, in die Gauß’sche Zahlenebene ein und vergleiche dann.
Wiederhole das Ganze mit der Zahl x = -2+i
Übungsaufgabe
|
|
2.3 Anwendung der komplexen Zahlen in der Physik
|

 

|
In der Physik werden komplexe Zahlen vielfältig verwendet wie z.B.:
• in der Quantentheorie die sehr effektiv das Werkzeug der komplexen Zahlen nutzt,
• in der Relativitätstheorie spielt die vierdimensionalen Raum-Zeit eine herausragende Rolle - in ihr
nutzt man als vierte Koordinate ict. Der Ausdruck r = (x,y,z,ict) wird als Vierervektor bezeichnet.
• die Behandlung von Differentialgleichungen zu Schwingungsvorgängen lässt sich wesentlich vereinfachen,
• komplizierten Beziehungen mit Produkten von Sinus- bzw. Kosinusfunktionen lassen sich durch
Einsatz der Exponentialfunktionen vereinfachen.
In der Elektrotechnik wird das kleine i schon für den Wechselstrom verwendet. Um Verwechslungen
zu vermeiden benutzt man für die imaginäre Einheit ein kleines j. Komplexe Zahlen haben daher die
Struktur a + b⋅j.
Benutzt wird die komplexe Zahlenebene, um Phasenverschiebungen z.B. bei kapazitiven oder induktiven
Lasten zu behandeln. So wird ein Ohmscher Widerstand entlang der reellen Achse, ein induktiver
Widerstand entlang der positiven imaginären Achse und ein kapazitiver Widerstand entlang der negativen
imaginären Achse abgetragen.
Freiwillig kann man noch den Artikel auf Wikipedia über Wechselstromrechnung durchlesen.
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



