|
3.1 Extremstellen
|

  
|
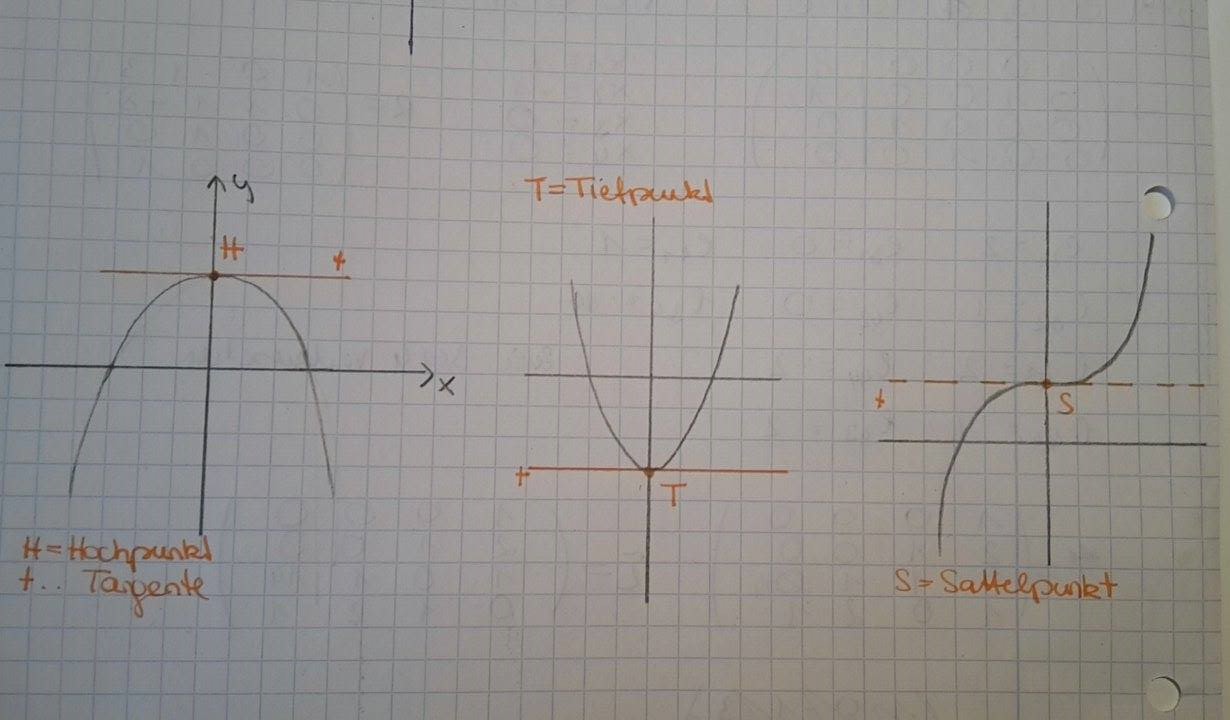
• Hochpunkt (lokales Maximum):
a < b und f(a) < f(b)
a > b und f(a) < f(b)
(alle y-Werte links und rechts vom Hochpunkt sind kleiner als f(b))
• Tiefpunkt (lokales Minimum):
a < b und f(a) > f(b)
a > b und f(a) > f(b)
(alle y- Werte links und rechts vom Tiefpunkt sind größer als f(b))
globales Extremum : Höchster oder tiefster Punkt in der Definitionsmenge Df.
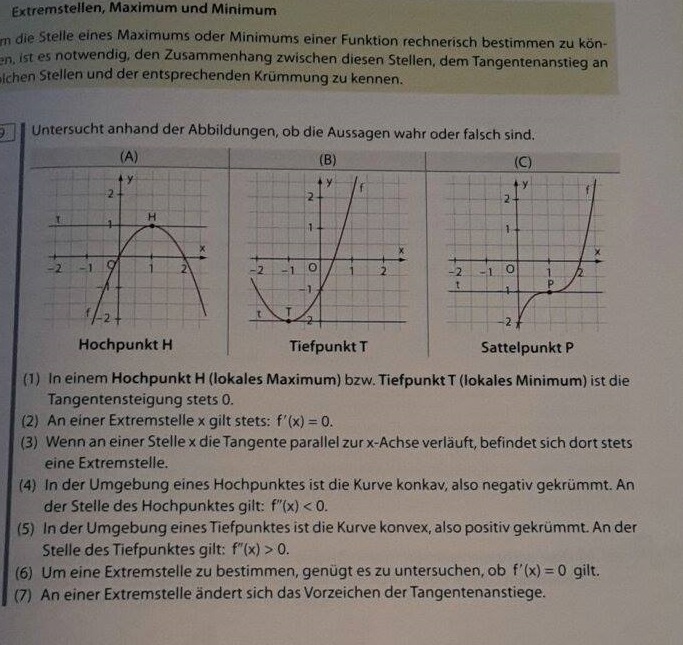
Liegt eine lokale Extremstelle vor, gilt f‘(x)=0.
Da durch die 1.Ableitung die Steigung der Tangente beschrieben werden kann.
Notwendige Bedingung :
Wir wissen:
Wenn an der Stelle x ein Extremwert vorliegt, dann ist f‘(x) = 0.
Wenn f‘(x)=0, dann liegt nicht notwendigerweise ein Extremwert vor. Es könnte sich auch um einen Sattelpunkt handeln.
Hinreichende Bedingung für Extremstellen :
x ist Hochpunkt: f‘(x)= 0 und f‘‘(x)< 0
x ist Tiefpunkt: f‘(x)= 0 und f‘‘(x)> 0
Die Tangente ist bei einer Extremstelle immer waagrecht.
|
|
3.3 Aufgaben
|

 

|
| 1)
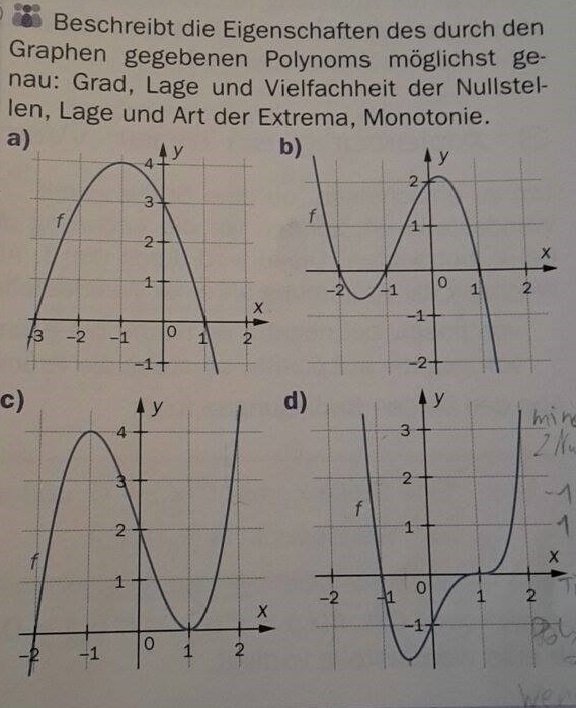
2) Berechne die lokalen Extrema der Funktion f(x)=x3-3x2+4 und untersuche das Monotonieverhalten!
3)
Hier sind die Lösungen!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



