|
4.1 Wendepunkt und Sattelpunkt
|

  
|
Wendepunkt :
An einer Wendestelle ändert sich die Krümmung der Funktion
Notwendige Bedingung :
Wenn ein Wendepunkt vorliegt ist f‘‘(x)= 0.
hinreichende Bedingung :
Ist f‘‘(x)=0 und f‘‘‘(x) ungleich 0, dann ist f ein Wendepunkt.
Sattelpunkt(Terrassenpunkt):
Ein Wendepunkt mit einer Tangente parallel zur x-Achse wird Sattelpunkt bzw. Terrassenpunkt genannt. Es gilt daher für solche Punkte: f '(x)=0 und f ''(x)=0.
|
|
4.2 Krümmung
|

  
|
Wenn die 1. Ableitung steigt, dann ist die Krümmung positiv.
Wenn die 1. Ableitung fällt, dann ist die Krümmung negativ.
Ist die Kurve negativ gekrümmt, so ist die 1. Ableitung fallend und die 2. Ableitung daher negativ.
Ist die Kurve positiv gekrümmt, so ist die 1. Ableitung steigend und die 2. Ableitung daher positiv.
Da sich im Wendepunkt die Krümmung ändert, hat die 1.Ableitung eine Extremstelle und die 2. Ableitung ist 0.
Eine zweimal differenzierbare Funktion f ist in einem Intervall I:
Positiv gekrümmt, wenn f‘‘(x)> 0 für alle x aus I
Negativ gekrümmt, wenn f‘‘(x)< 0 für alle x aus I
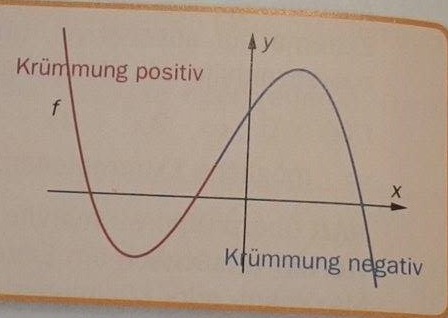
Merkhilfe:
Rechts gekrümmt= negative Krümmung (trauriger Smiley)
Links gekrümmt= positive Krümmung (glücklicher Smiley)
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



