Ein einfaches Beispiel für einen linearen Zusammenhang kann eine Zahlenfolge sein.
Ein Beispiel wäre die Folge:
2 , 5 , 8 , 11 , ...
Diese Folge solltest du ohne Schwierigkeiten fortsetzen können!
Die Lösung ist natürlich ... , 14 , 17 , 20 , ...
Überlege nun kurz, wie du die Folge beschreiben würdest!
Eine Möglichkeit wäre: "Die Folge startet mit 2 und mit jedem Folgelied nimmt der Wert um 3 zu."
Etwas schwieriger wird es, wenn man diese Beschreibung mit einer mathematischen Formel ausdrücken möchte.
Dafür nenne ich das Folgeglied "F" und den Wert des Folgeglieds "W". Also:
F ... das wievielte Folgeglied (oder Nummer des Folgeglieds)
W ... der Wert des Folgeglieds
Für eine bessere Übersicht, tabelliere ich die Folgeglieder und deren Werte.

Die Formel die ich suche, muss also für alle F und W dieser Tabelle stimmen.
Durch Überlegen kommt man auf die Formel W = 3 · F - 1 .
Da der Wert von der Nummer des Folgeglieds abhängig ist schriebt man auch
W(F) = 3 · F - 1 , also Wert, in Abhängigkeit von der Nummer des Folgeglieds.
Einerseits kann man nun überprüfen ob die Formel richtig ist, indem man einsetzt und das Ergebnis mit der Tabelle vergleicht:
F = 1: W(1)=3 · 1 - 1 = 2 ✔
F = 2: W(2)=3 · 2 - 1 = 5 ✔
F = 3: W(3)=3 · 3 - 1 = 8 ✔
...
Andererseits kann man auch für dehr späte Folgeglieder den Wert bestimmen.
Etwa lässt sich der Wert des 2500sten Folgeglied mit
W(2500) = 3 · 2500 - 1 = 7499
berechnen.
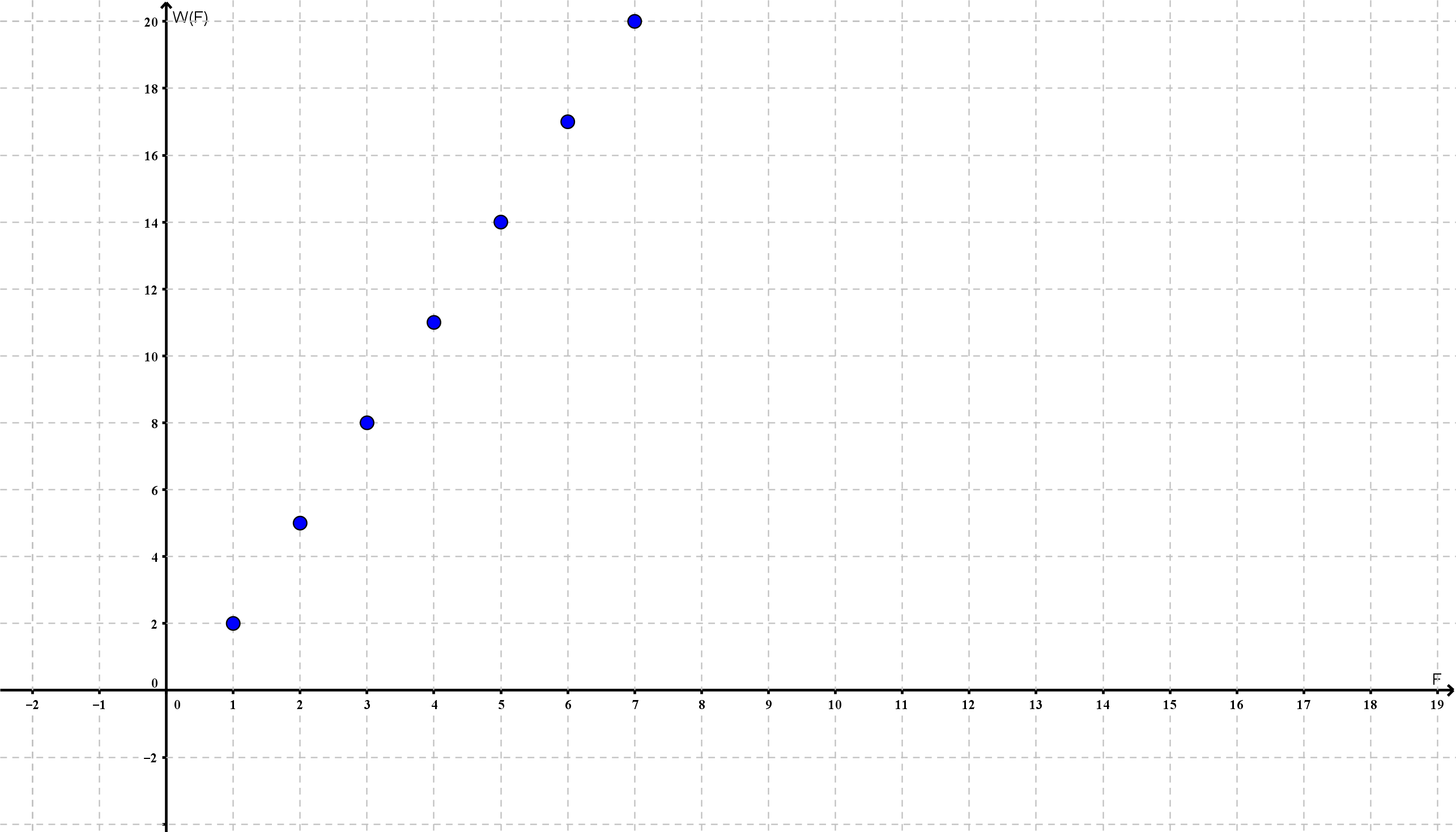
Warum man diesen Zusammenhang als "linear" bezeichnet wird klar, wenn man die Punkte der Tabelle in ein Koordinatensystem einzeichnet.
Lernstoff
|



