|
4.1 Wichtige Eigenschaften
|

  
|
- Die Funktionsgleichung einer Logarithmusfunktion hat folgende Form: f(x) = loga (x) , wobei a > 0 die Basis heißt.
- Die Definitionsmenge der Logarithmusfunktion ist die Menge der positiven reellen Zahlen .
Die Bildmenge der Logarithmusfunktion ist die gesamte Menge der reellen Zahlen.
- Der Graph jeder Logarithmusfunktion (unabhängig von der Basis) verläuft durch den Punkt P(1/0).
- Die Logarithmusfunktion loga (x) ist die Umkehrfunktion der Exponentialfunktion mit Basis a.
- f(x) = ln(x) nennt man auch die natürliche Logarithmusfunktion (oder ln-Funktion) . Sie ist die Umkehrfunktion der Exponentialfunktion zur Basis e.
Überprüfe deine Ableitungs-Kenntnisse:
MultipleChoice
|
|
4.2 Beispiele von Logarithmusfunktionen
|

 
|
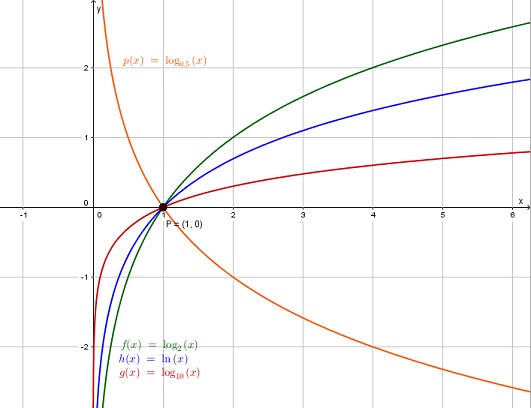
- So sehen Logarithmusfunktionen mit verschiedener Basis aus:
a= 0,5 ⇒ f(x) = log0,5 (x)
a=2 ⇒ f(x) = log2 (x)
a=10 ⇒ f(x) = log10 (x)
f(x) = ln(x)
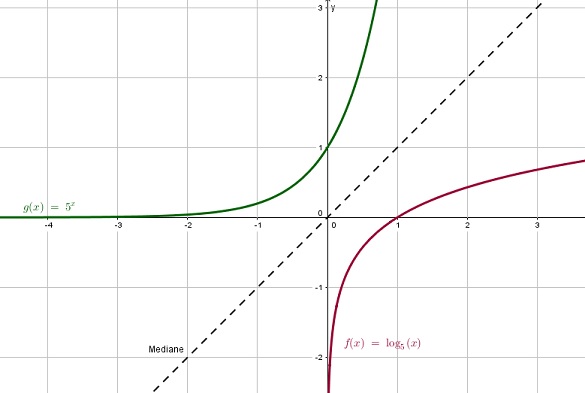
- So sieht eine Logarithmusfunktion mit ihrer Umkehrfunktion aus:
Zur Erinnerung:
Eine Funktion f und ihre Umkehrfunktion f -1 spiegeln sich an der 1. Mediane.
f(x) = log5 (x)
⇒ f -1 (x) = 5x
|
|
4.3 Ableitung der Logarithmusfunktion
|

 

|
Mit der folgenden Simulation wird die Ableitungsfunktion von natürlichen Logarithmusfunktionen dargestellt.
Versuche zu erkennen, welche spezielle Funktion diese Ableitungsfunktion ist.
Hier
kommst du zur Simulation!
Vorgriff
|
|
4.4 Durchgerechnetes Beispiel einer Kurvendiskussion
|

 
|
Kurvendiskussion der ln - Funktion f:
f(x) = ln(x² + 16)
- Definitionsmenge:
Die Definitionsmenge umschließt die gesamte Menge der reellen Zahlen.
(Da x²+16 nie = 0 werden kann)
- Nullstellen berechnen:
f(x) = 0 ⇔
ln(x² + 16) = 0 ⇔
x² + 16 = 1 ⇔
x² = -16 ⇒ es existiert keine Nullstelle im reellen Bereich
- Extremwerte bestimmen:
f' (x) = 0 ⇔
2x / (x²+16) = 0 ⇔
2x = 0 ⇔
x = 0
⇒Es existiert eine Extremstelle E(0|2,77)
Überprüfen ob es Hoch- oder Tiefpunkt ist:
f''(0) = 0,125 > 0
⇒ Die Funktion hat einen Tiefpunkt T(0 | 2,77)
- Wendepunkte bestimmen:
f''(x) = 0 ⇔
-2(x²-16) / (x²+16)² = 0 ⇔
x² - 16 = 0 ⇔
x² = 16 ⇔
x1 = 4
x2 = -4
Überprüfen ob es wirklich Wendepunkte sind:
f'''(4) = -0,0156 ≠ 0 ⇒ es ist ein Wendepunkt
f'''(-4) = 0,0156 ≠ 0 ⇒ es ist ein Wendepunkt
⇒ Die Funktion f besitzt zwei Wendepunkte: W1 (4 | 3,47) un W2 (-4 | 3,47).
- Tangentensteigung:
Setze die x-Werte der Wendepunkte in die 1. Ableitung ein:
f'(4)= 0,25
f' (-4) = -0,25
- Graph zeichnen:
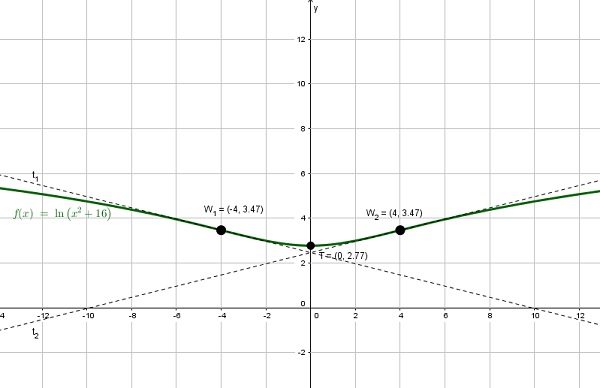
- Monotonieverhalten:
Die Funktion f ist monoton fallend im Intervall: ( -∞ ; 0).
Die Funktion f ist monoton steigend im Intervall: (0 ; ∞)
- Krümmungsverhalten:
Die Funktion f ist negativ gekrümmt in den Intervallen: ( -∞ ; -4) und (4; ∞)
Die Funktion f ist positiv gekrümmt im Intervall: (-4 ; 4)
- Symmetrie
Die Funktion f ist symmetrisch bezüglich der y-Achse.
Beweis:
zz.: f(x) = f(-x)
⇔ ln(x²+16) = ln( (-x)²+16)
Da (-x)² = x² gilt:
ln(x²+16) = ln( (-x)²+16) ⇔ ln(x²+16) = ln(x²+16)
und somit gilt:
f(x) = f(-x) ∀ x ∈ D.
- Asymptotisches Verhalten:
Wie verhält sich die Funktion im Unendlichen?
lim(x→ ∞) (ln(x² + 16)) = "ln(∞)" = ∞
lim(x→ -∞) (ln(x² + 16)) = "ln(∞)" = ∞
|
|
4.5 Hausübung: Führt eine vollständige Kurvendiskussion einer ln - Funktion durch.
|

 

|
Als Hausübung sollt ihr nun selbstständig eine Kurvendiskussion durchführen.
Die Funktion lautet: f(x) = x² * ln(x+2).
Bitte lade deinen Graphen wieder als GeoGebra Datei in der Moodle Platform "7.Einheit" hoch.
Hier
geht's zur Platform!
Viel Erfolg. :)
Hausaufgabe
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



