4.1 Ungleichungen
http://www.mathe-online.at/materialien/ppvo/files/ungleichungen-exkurs.html
|

 
|
Klick den obenstehenden Link an, wenn du noch Unklarheiten zum Thema Ungleichungen hast; dort findest du die eine Erklärung zu Ungleichungen.
Was passiert bei folgenden Rechenoperationen mit der Ungleichung:
- Seiten vertauschen
- Addition/Subtraktion der gleichen Zahl/des gleichen Terms
- Multiplikation/Division mit positiver Zahl
- Multiplikation/Division mit negativer Zahl
Die Lösungen dazu findest du in folgenden Rechenregeln
|
|
4.4 Fortlaufende Ungleichungen
|

 
|
Die folgenden Ungleichungen
-3<2x+1£5x-1
kann man in zwei Ungleichungen auflösen. Sind die beiden mit UND oder ODER verbunden? Löse die Aufgabe!
|
|
4.5 Betragsungleichungen
|

 
|
Weißt du, was folgender Ausdruck bedeutet?
½-5½
Die Striche links und rechts von -5 nennt man Betragsstriche und bedeuten, dass das Vorzeichen der Zahl weggelassen werden muss.
Das heißt:
½-5½=5
½5½=5
Formal ausgedrückt wird dies so:
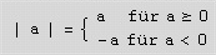
Andere Ausdrücke für |x|<2 sind:
-2 < x < 2 oder
-2 < x Ù x < 2
Aus dem letzten Ausdruck wird auch schon klar, wie man Betragsungleichungen lösen kann. Versuch es bei folgenden Beispielen:
|7-2x| < |x+1|
|2| £ |x-3| < 4
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



