|
8.1 Einführungbeispiel
|

 

|
Für einen Wanderweg, der von Altaussee nach Hallstadt führt, zeigt die nebenstehende Karte die Höhenmeter an, welche überwinden werden müssen. Auf der senkrechten Achse wird die Höhe aufgetragen und auf der waagrechten Achse sind die zurückgelegten Kilometer abzulesen.
Wie weit ist ein Wanderer gegangen wenn er sich auf (a) 600m (b) 700m Höhe befindet?

Eintrag in das Lerntagebuch
|
|
8.3 Begründe!
|

 

|
Welche dieser Diagramme sind injektiv, surjektiv oder sogar bijektiv?
Begründe deine Entscheidung!
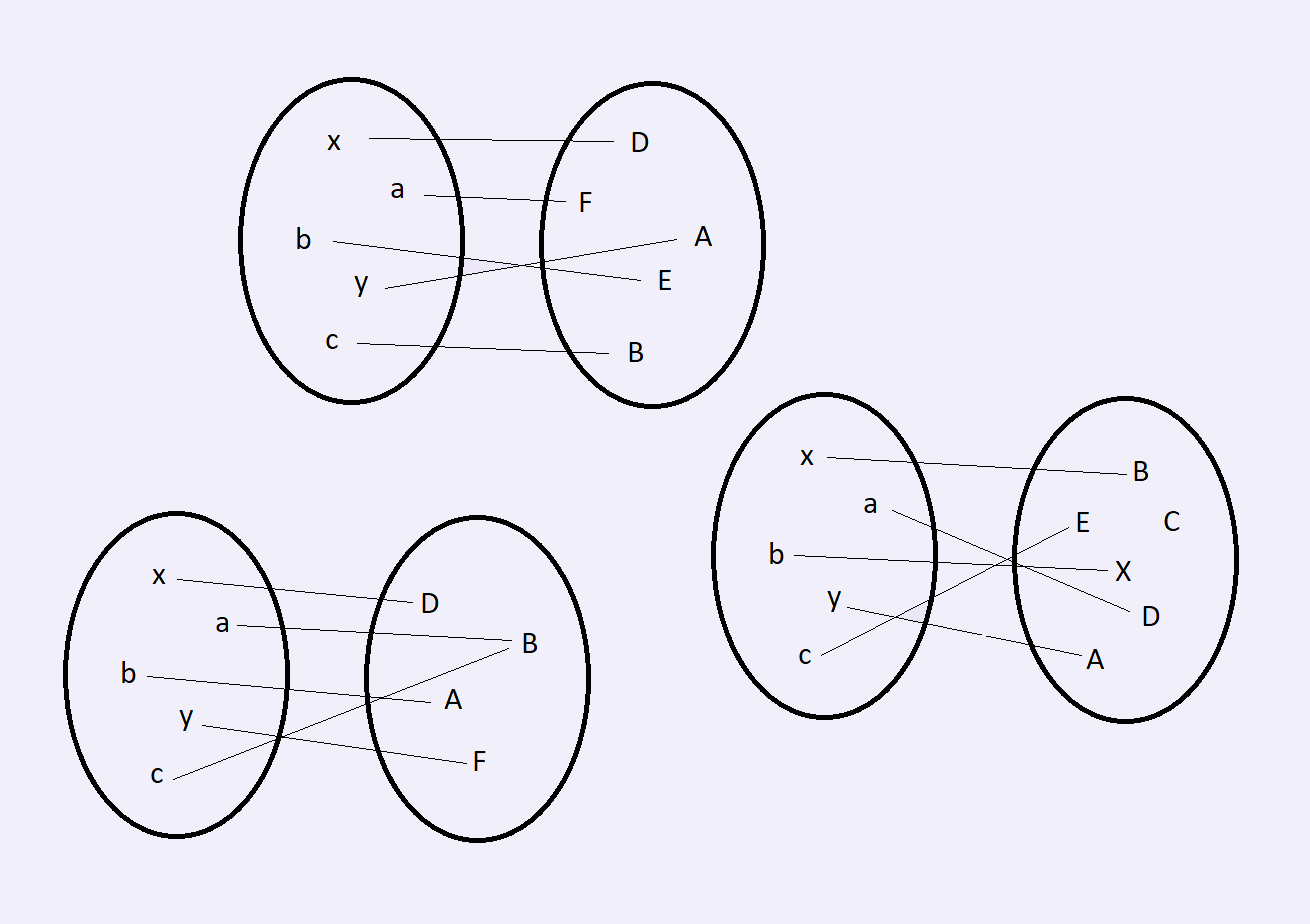
Eintrag in das Lerntagebuch
|
|
8.4 Übungsaufgabe
|

 


|
Oft kann eine waagrechte Gerade bei der Bestimmtung von Injektivität und Surjektivität hilfreich sein!
Falls es keine waagrechte Gerade gibt, so dass diese die Funktion in mehr als einem Punkt schneidet, ist die Funktion injektiv.
Falls es keine waagrechte Gerade gibt, so dass diese die Funktion nicht schneidet ist die Funktion surjektiv.
Bestimme Injektivität und Surjektivität der Funktionen mithilfe der Geraden h. Nimm für die Funktionen als Definitions- und Wertemege die reellen Zahlen an. Spiele dafür ein wenig mit dem Schieberegler um mehrere Geraden auszuprobieren.
Eintrag in das Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



