|
2.1 Pythagoras
|

 

|
Pythagoras war ein griechischer Mathematiker, der auf der Insel Samos geboren wurde
und zahlreiche Länder, unter anderen Ägypten, Babylonien, Arabien und Indien bereiste.
Er lebte etwa 570-497 v. Chr. und er gründete eine Philosophenschule in Unteritalien.
Der Lehrsatz des Pythagoras zählt wegen seiner großen Bedeutung für Berechnungen in der Geometrie
zu den berühmtesten mathematischen Lehrsätzen. Die Bezeichnung "pythagoräischer Lehrsatz" ist
nicht ganz korrekt, da dieser Zusammenhang bereits lange vor Pythagoras den Ägyptern (Nilvermessung),
Babylonien, Indern und Chinesen bekannt war. Ein Beweis des Lehrsatzes wurde erst von den
Schülern des Pythagoras gefunden. Heute sind uns 370 Beweise bekannt.

|
|
2.3 Herleitung ins Schulübungsheft
|

 

|

Konstruiere ein Dreieck mit den Seitenlängen a = 3cm, b = 4cm und c = 5cm!
Zeichne dann über jede Dreiecksseite ein Quadrat!
Du könntest die Quadrate mit den erforderlichen Seitenlängen aus kariertem
Papier ausschneiden und dann aufkleben.
Vergleiche die Summe der Flächeninhalte der beiden kleineren Quadrate mit
dem Flächeninhalt des großen Quadrats!
Was fällt dir auf?
Versuche das Gleiche bei einem Dreieck mit den Seitenlängen a = 2cm, b = 3cm und c = 4cm!
Fällt dir nun etwas auf? Gibt es einen Unterschied? Wenn JA, welchen?
Lernstoff
|
|
2.4 Lösung - Der Lehrsatz des Pythagoras
|

  
|
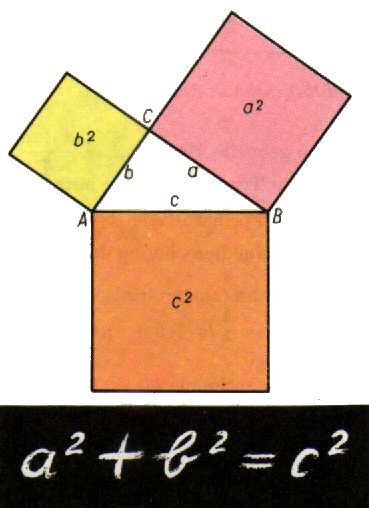
Wenn ein Dreieck rechtwinklig ist, dann ist die Summe der Flächeninhalte
der Kathetenquadrate gleich dem Flächeninhalt des Hypothenusenquadrats.
a² + b² = c²
Das erste Dreieck, dass du oben zeichnen solltest, ist rechtwinklig, das heißt,
dass die Summe der Flächeninhalte der beiden kleineren Quadrate gleich dem
Flächeninhalt des großen Quadrates ist.
Das zweite Dreieck hingegen ist kein rechtwinkliges Dreieck, deswegen
gilt hier der Lehrsatz des Pythagoras nicht!
|
|
2.6 Abwechslung
|

 

|
Zur Abwechslung versuch dich doch an einem Sudoku!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



