|
5.1 Kathetensätze
|

  
|
In einem rechtwinkligen Dreieck gibt es noch zwei weitere sehr interessante
und praktische Sätze: den Höhensatz und die Kathetensätze.
Dazu betrachten wir kurz die Höhe h auf die Hypotenuse c in einem rechtwinkligen Dreieck:
Mache dir im Schulübungsheft eine Skizze und schreibe dir die Herleitung auf!
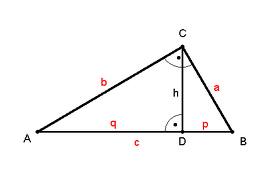
Die Höhe h teilt die Hypotenuse c in zwei Abschnitte, die so genannten Hypotenusenabschnitte p und q.
Dabei liegt p an die Seite a an und q an die Seite b.
Durch das Einzeichnen der Höhe h sind zwei weitere Dreiecke entstanden, die zum Ausgangsdreieck ähnlich sind.
Also: 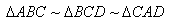 Diese Ähnlichkeit verwenden wir nun:
1)
Diese Ähnlichkeit verwenden wir nun:
1) 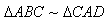 c : b = b : q und durch Umformen: b² = c·q
2)
c : b = b : q und durch Umformen: b² = c·q
2) 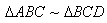 c : a = a : p und durch Umformen: a² = c·p
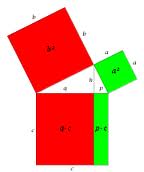
Auch diese Sätze kann man durch Flächeninhalte darstellen:
c : a = a : p und durch Umformen: a² = c·p
Auch diese Sätze kann man durch Flächeninhalte darstellen:
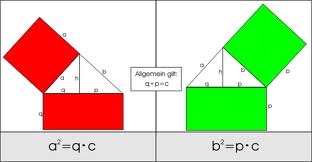 In dieser Abbildung kann man die Kathetensätze und den pythagoräischen Lehrsatz ablesen!
Einen allgemeinen Beweis hast du schon im Abschnitt über die Beweise des Satzes des
Pythagoras kennen gelernt, nämlich den Scherungsbeweis!
Sie dir nochmals kurz die Animation dieses Beweises an!
In dieser Abbildung kann man die Kathetensätze und den pythagoräischen Lehrsatz ablesen!
Einen allgemeinen Beweis hast du schon im Abschnitt über die Beweise des Satzes des
Pythagoras kennen gelernt, nämlich den Scherungsbeweis!
Sie dir nochmals kurz die Animation dieses Beweises an!
Lernstoff
|
|
5.2 Abwechslung
|

 

|
Zur Abwechslung kannst du dich an einem Sudoku versuchen!
|
|
5.3 Höhensatz
|

  
|
Neben den Kathetensätzen gibt es auch noch den Höhensatz, in dem
die Hypotenusenabschnitte p und q Anwendung finden. Mache dir auch zu diesem Abschnitt Notizen ins Schulübungsheft
Wir nutzen nocheinmal die Ähnlichkeit zweier Dreiecke aus:
 Dabei gilt:
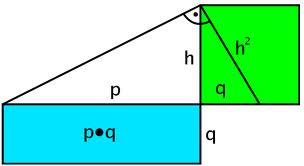
Dabei gilt:  q : h = h : p und durch Umformen: h² = p·q
Auch dieser Sätz lässt sich durch Flächen darstellen:
q : h = h : p und durch Umformen: h² = p·q
Auch dieser Sätz lässt sich durch Flächen darstellen:
Lernstoff
|
|
5.5 Einführungsbeispiel
|

  
|
Im nächsten Abschnitt sollst du Beispiele berechnen.
Dazu gibt es hier ein Einführungsbeispiel:
Von einem rechtwinkligen Dreieck ABC sind die Längen einer Kathete (a=13.6cm) und des
anliegenden Hypotenusenabschnitts (p=6.4cm) gegeben. Wie lang sind die fehlenden Seiten?
 Die gesuchten Seitenlängen betragen also b = 25.5 cm und c = 28.9 cm.
Du siehst, dass du die Lehrsätze dieses Lernpfades in den Beispielen unterschiedlich einsetzen musst
und die Formeln umformen musst um eine bestimmte Größe ausrechnen zu können!
Die gesuchten Seitenlängen betragen also b = 25.5 cm und c = 28.9 cm.
Du siehst, dass du die Lehrsätze dieses Lernpfades in den Beispielen unterschiedlich einsetzen musst
und die Formeln umformen musst um eine bestimmte Größe ausrechnen zu können!
Übungsaufgabe
|
|
5.6 Beispiele
|

 

|
Auch zu diesem Abschnitt und den obigen Sätzen gibt es nun einige Übungsbeispiele
6 Beispiele sind wieder ins Schulübungsheft zu machen und der Rest als Hausübung ins Hausübungsheft!
 Zum Vergleich die Lösungen
Zum Vergleich die Lösungen
Übungsaufgaben
|
|
5.8 Abschluss
|

 
|
Nun hast du den gesamten Lernpfad gemeistert!
Gratuliere!
 Wenn du noch Lust hast, kannst du dich noch einmal an einem Sudoku versuchen! Viel Spaß!
Wenn du noch Lust hast, kannst du dich noch einmal an einem Sudoku versuchen! Viel Spaß!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



