|
3.1 Vorbemerkung
|

 

|
Zieht man auf beiden Seiten etwa der Gleichung x² = 4 die (Quadrat-) Wurzel, so erhält man
x = 2. Tatsächlich ist jedoch auch -2 eine Lösung der Gleichung x² = 4, wie man
durch die Probe sofort bestätigt. Beidseitiges Wurzelziehen einer Gleichung ist keine
Äquivalenzumformung!
Die beim Wurzel ziehen erhaltene positive Lösung ist anschließend durch die negative Lösung -2 zu ergänzen.
|
|
3.2 Nullstellen einer quadratischen Funktion
|

 

|
Die Nullstellen einer quadratischen Funktion sind die Lösungen. Man setzt y=0

Da es nicht immer einfach ist die Methode des Ergänzens auf ein volles Quadrat anzuwenden, behilft man sich mit Lösungsformeln.
|
|
3.3 Lösungsformel
|

  
|

Um eine Lösungsformel anzuwenden betrachtet man zuerst die zu lösende quadratische Gleichung.Man formt so lange um bis alle x² und x und Zahlen zusammengefasst sind.
Steht vor dem x² noch eine Zahl(Konstante) wie z.B. 3x² so verwendet man die Allgemeine Form, uns setzt a=3
Denn a und b sind die Zahlen VOR dem x² bzw. x.
c ist immer die Zahl ohne x.
Im Beispiel oben formen wir die Zeile x² - x = 6 auf x² -x - 6 = 0 um, um eine Lösungsformel zu verwenden.
Wir verwenden die Normalform da vor dem x² keine Zahl steht.
p = (-1) Achtung Vorzeichen müssen mitgenommen werden 1·x = x und (-1)·x = -x
q = (-6)
So erhält man als Lösung L = {-3,2}
Man hätte auch die Allgemeine Form verwenden können:
a = 1
b = (-1)
c = (-6)
So erhält man als Lösung L = {-3,2} (gleich wie zuvor)
Man sieht beide Formeln führen zum Erfolg.
|
|
3.4 Geometrische Interpretation
|

  
|
In der Grafik kann man leicht erkennen das x=-3 und x=2 die Nullstellen sind.
Um den Grafen ins Heft zu zeichnen benutzt man eine Wertetabelle.Man schreibt x-Werte von z.B. -3,-2,-1,0,1,2,3 (oder auch mehr Zahlen)und rechnet dazu die passenden y-Werte (0,-8,-1,-12,-12,-8,0,12).
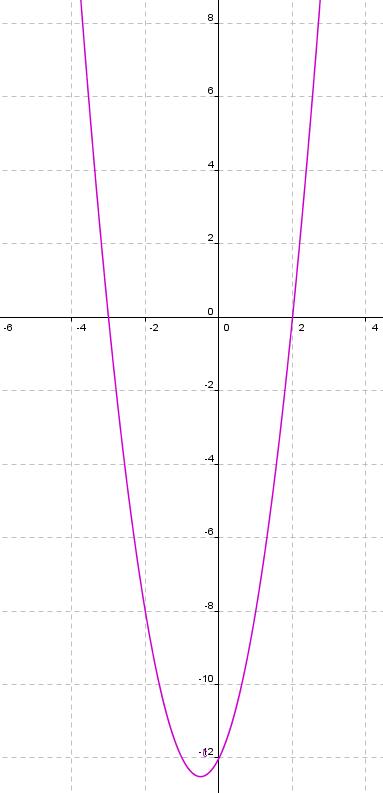
Wertetabelle:

So wird die Wertetabelle ins Heft gezeichnet, in die jeweiligen werte in ein Koordinatenkreuz eingezeichnet.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



