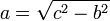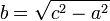Generelles
Ein rechtwinkliges Dreieck ist eine geometrische Figur mit
drei Seiten und
drei Winkel. Die Scheitel der Winkel werden als
Eckpunkte bezeichnet. Beim rechtwinkligen Dreieck gibt es nun eine Besonderheit: einer der Winkel ist
ein rechter Winkel; d.h. er betragt genau neunzig Grad. Dadurch, dass er ein Winkel ein rechter Winkel ist, hat man den Seiten des Dreiecks besondere Namen gegeben.
Die
Hypotenuse ist die Seite die dem rechten Winkel gegenueber liegt. Sie ist die
langste Seite des Dreiecks und wird normalerweise als die Seite
c bezeichnet. Die
Katheten sind die beiden kuerzeren Seiten die an den rechten Winkel anliegen.
Umfang und Flaecheninhalt
Den
Umfang des rechtwinkligen Dreiecks errechnet man sich, indem man alle drei Seiten
a , b und c addiert.
U = a + b + c
Der
Flaecheninhalt leitet sich vom Flaecheninhalt des Rechtecks her. Davon erfahrst du in Kapitel 3 dieses Lernpfades. Die Formel lautet:
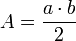 Der Satz des Pythagoras
Der Satz des Pythagoras
Der
Satz des Pythagoras beschreibt die Beziehung zwischen den Seiten des rechtwinkligen Dreiecks. Durch ihn kann man sich die dritte Seite errechnen, wenn man die
Länge der anderen zwei Seiten gegeben hat. Er lautet wie folgt.

Um nun auf die Seite
c zu kommen zieht man noch
die Wurzel:
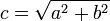
Fuer die anderen zwei Seiten gilt durch Umformen dann folgendes: