|
2.3 Berechnung eines Vektors aus Anfangs- und Endpunkt
|

  
|
Gegeben sind die Punkte  . .
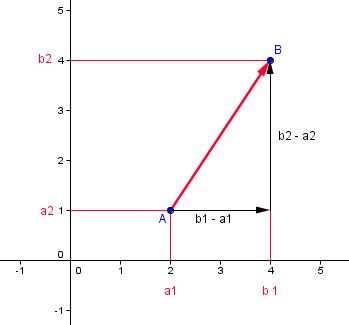
Aus der Zeichnung kann man nun folgendes ablesen:
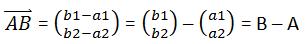
In dieser Zuordnungsübung kannst du die Strecke zwischen zwei Punkten berechnen und ihr einen Vektor zuordnen.
Wiederholung, Selfchecking Test
|
|
2.4 Addition und Subtraktion von Vektoren
|

  
|
Vektoren rechnerisch zu addieren, haben wir ja bereits ausführlich geübt.
Damit du dir die Addition aber auch grafisch vorstellen kannst, ist hier noch einmal die geometrische Darstellung der Addition erklärt!
Gegeben sind folgende zwei Vektoren: 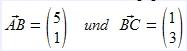 Nun addieren wir sie:
Nun addieren wir sie: 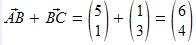 Wenn wir diese Addition zuerst umformen, erhalten wir:
Wenn wir diese Addition zuerst umformen, erhalten wir: 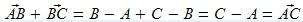 Also erhalten wir:
Also erhalten wir: 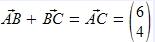 Hier ist dieser Zusammenhang grafisch dargestellt:
Hier ist dieser Zusammenhang grafisch dargestellt:
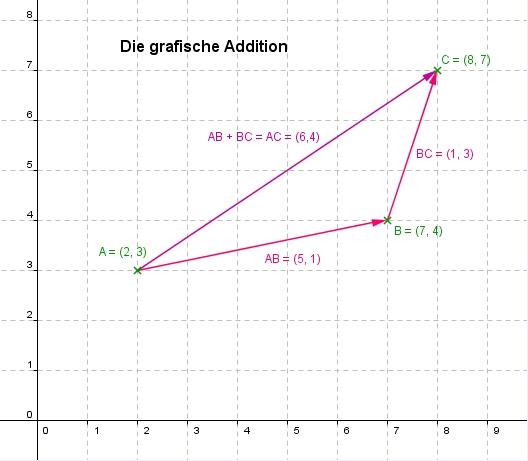 Die Subtraktion kann man als Addition mit einem negativen Vektor verstehen.
Wir nehemen die gleichen Vektoren und subtrahieren diese:
Die Subtraktion kann man als Addition mit einem negativen Vektor verstehen.
Wir nehemen die gleichen Vektoren und subtrahieren diese: 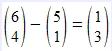 Grafisch sieht das dann so aus:
Grafisch sieht das dann so aus:
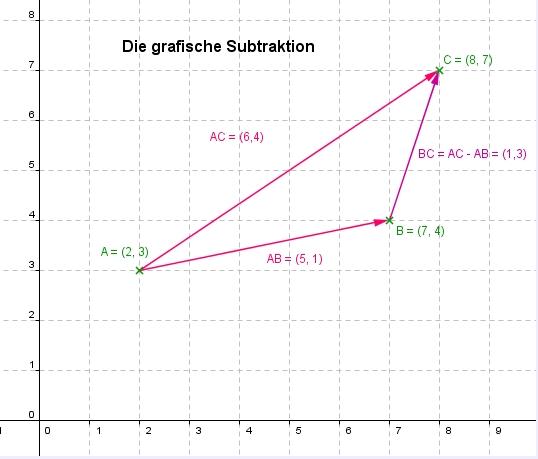
Wiederholung, Lernstoff
|
|
2.6 Ein Beispiel
|

 

|
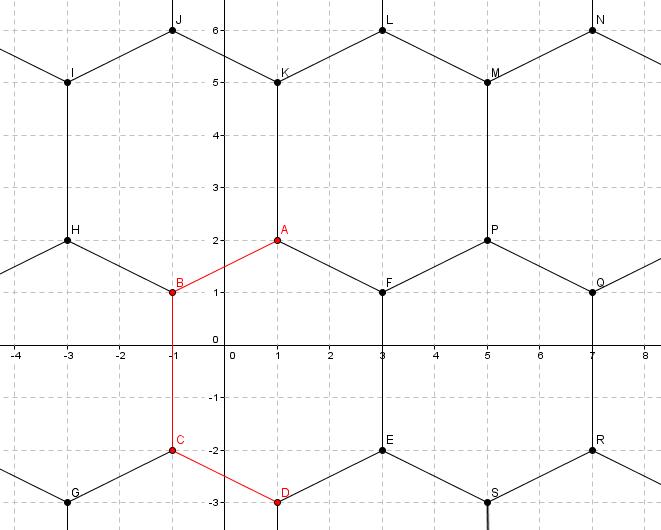
Von dem hier abgebildeten "Parkettmuster" kennt man die Punkte 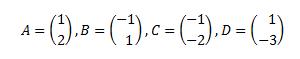 .
Berechne die Punkte E, F, G, H, I, J, K, L, M, N, P, Q, R, S! .
Berechne die Punkte E, F, G, H, I, J, K, L, M, N, P, Q, R, S!
Übungsaufgabe, Heft
|
|
2.7 Freiwillige vor!
|

 

|
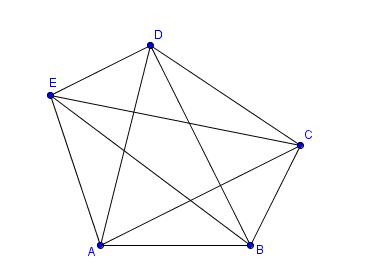
Diese Figur kann auf verschiedene Arten durch vier Vektoren festgelegt werden.
Gib auf zwei verschiedene Arten vier solche Vektoren an (siehe Skizze!).
Drücke dann die restlichen "Seitenvektoren" und "Diagonalvektoren" durch diese vier Vektoren aus!
Hier findest du das Lösungsblatt dazu!
Übungsaufgabe, Heft
|
|
2.8 Parallelogramm- und Differenzregel
|

  
|
Hier findest du noch einmal die Grundgesetze der Addition veranschaulicht wieder. Lies sie dir genau durch!
Drücke nun die in folgender Abbildung dargestellten Vektoren c und d jeweils durch a und b aus!
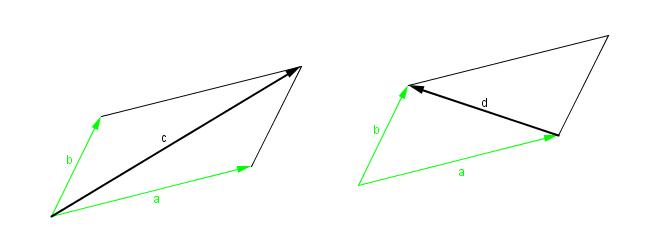 Lösung:
Lösung:
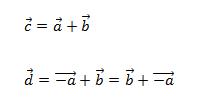 Zusammengefasst bedeutet das also:
Zusammengefasst bedeutet das also:
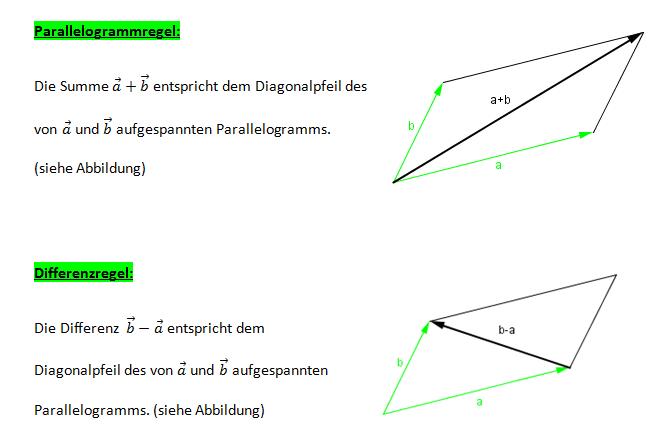
Lernstoff
|
|
2.9 Addition und Subtraktion von Vektorpfeilen
|

 

|
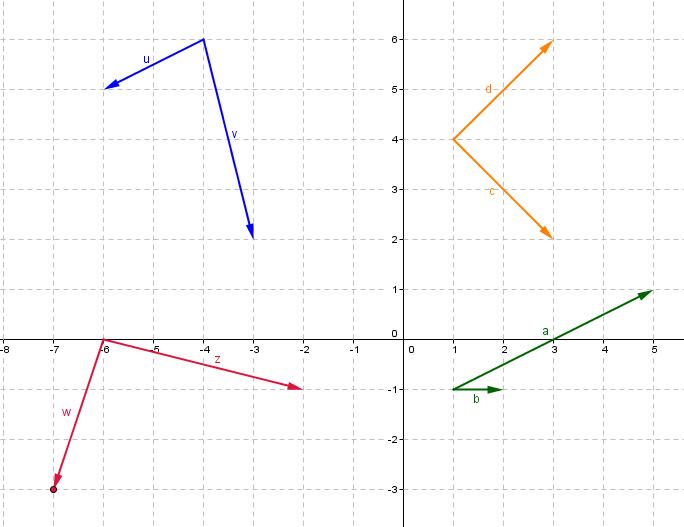 1) Zeichne diese Vektoren in dein Heft!
2) Lies aus der Zeichnung die Koordinaten der Vektoren
1) Zeichne diese Vektoren in dein Heft!
2) Lies aus der Zeichnung die Koordinaten der Vektoren 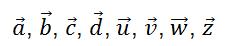 ab!
2) Berechne nun folgende Vektoren: ab!
2) Berechne nun folgende Vektoren: 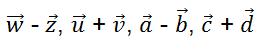 !
3) Trage die berechneten Vektoren in die Zeichnung in deinem Heft ein! !
3) Trage die berechneten Vektoren in die Zeichnung in deinem Heft ein!
Übungsaufgabe, Heft
|
|
2.10 Ein Beispiel
|

 

|
Ein Parallelogramm hat die Eckpunkte A=(1/1), B=(4/1), C=(6/3), D=(3/3).
1) Überzeuge dich durch Zeichnung und Rechnung, dass es sich dabei tatsächlich um ein Parallelogramm handelt!
(Zeige dazu 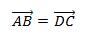 !)
2) Überprüfe durch Rechnung die Parallelogrammregel !)
2) Überprüfe durch Rechnung die Parallelogrammregel 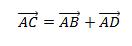
Übungsaufgabe, Heft
|
|
2.11 Geometrische Darstellung der Multiplikation eines Vektors mit einer reellen Zahl
|

  
|
Erklärung anhand eines Beispiels:

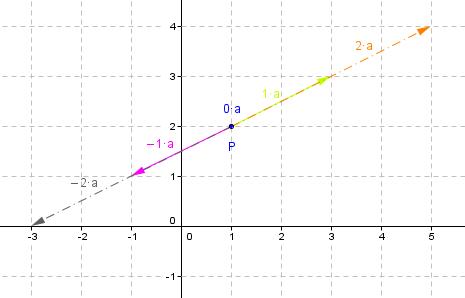 Lösung:
Lösung:
 Hier ist ein Merksatz der das Wichtigste noch einmal zusammengefasst:
Wird ein vom Nullvektor verschiedener Vektor aus R² durch einen Pfeil in der Ebene dargestellt,
dann entspricht die Multiplikation dieses Vektors mit einer reellen Zahl r eine Streckung des
Pfeils mit dem Faktor r.
Hier ist ein Merksatz der das Wichtigste noch einmal zusammengefasst:
Wird ein vom Nullvektor verschiedener Vektor aus R² durch einen Pfeil in der Ebene dargestellt,
dann entspricht die Multiplikation dieses Vektors mit einer reellen Zahl r eine Streckung des
Pfeils mit dem Faktor r.
Lernstoff
|
|
2.12 Beispiele
|

 

|
1.
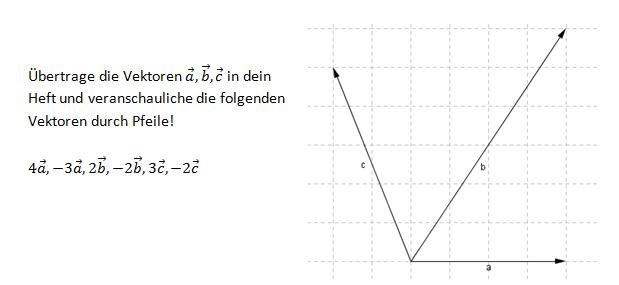 2.
2.
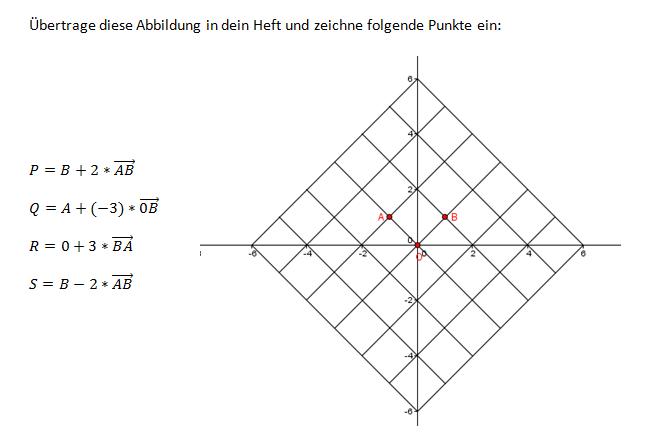
Übungsaufgabe, Heft
|
|
2.13 Beschreibung von Strecken
|

 

|
In einem Parallelepiped ABCDEFGH (=vierseitiges, schiefes Prisma, dessen Grund- und Deckflächen Parallelogramme sind)
sei 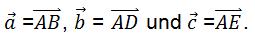
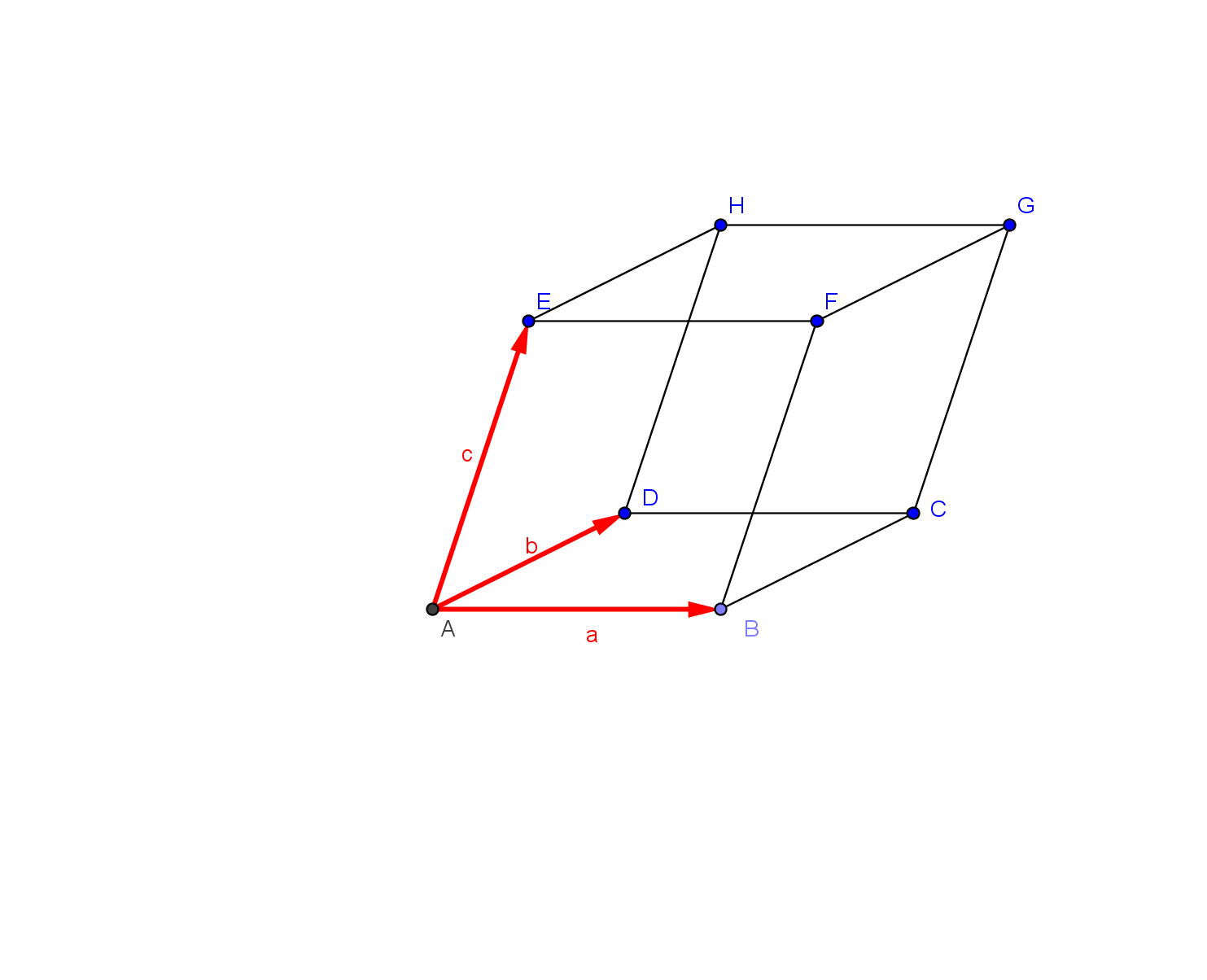 a) Zeichen dieses Parallelepiped mit Geogebra.
b) Druck deine Zeichnung aus und klebe sie in dein Schulübungsheft.
c)
a) Zeichen dieses Parallelepiped mit Geogebra.
b) Druck deine Zeichnung aus und klebe sie in dein Schulübungsheft.
c) 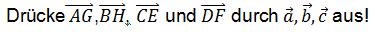 und schreibe dein Ergebnis ebenfalls in dein Schulübungsheft. und schreibe dein Ergebnis ebenfalls in dein Schulübungsheft.
Übungsaufgabe
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



