|
2.1 Grundlegendes zu Sinus,Cosinus, Tangens
|

 

|
Sinus, Cosinus und Tangens können jeweils als Verhältnis der Seitenlängen zueinander betrachtet werden.
Voraussetzung für Sinus, Cosinus und Tangens ist ein rechtwinkeliges Dreieck.
Folgende Skizze dient als Skizze für die folgenden Definitionen von Sinus, Cosinus und Tangens.

|
|
2.2 Sinus
|

 

|
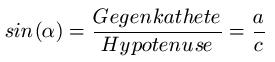
Anmerkungen:
1)Für α wird ein Winkel in Grad eingesetzt.
2)Verwende nur Längen der Gleichen Einheit (z.B. cm oder m)
3)Pass auf, dass dein Taschenrechner beim rechnen auf DEG (Degree) eingestellt ist.
4)Wenn du den Sinuswert eines Winkels kennst und den Winkel berechnen wills, dann musst du die Umkehrfunktion des Sinus, naemlich den arcsin, verwenden.
Beispiel 3: Berechne in deinem Heft den Winkel α wenn a=3cm und c=5cm.
|
|
2.3 Kosinus
|

 

|
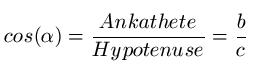
Anmerkungen:
1)Für α wird ein Winkel in Grad eingesetzt.
2)Verwende nur Längen der gleichen Einheit.
3)Pass auf, dass dein Taschenrechner beim rechnen auf DEG (Degree) eingestellt ist.
4)Wenn du den Cosinuswert eines Winkels kennst und den Winkel berechnen willst, dann musst du die Umkehrfunktion des Kosinus, naemlich den arccos, verwenden.
Beispiel 4: Berechne in deinem Heft den Winkel α wenn die Ankathete 3 cm und die Hypotenuse 5 cm lang ist.
|
|
2.4 Tangens
|

  
|
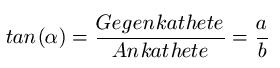
Anmerkungen:
1)Für α wird ein Winkel in Grad eingesetzt.
2)Verwende nur Längen der gleichen Einheit.
3)Pass auf, dass dein Taschenrechner beim rechnen auf DEG (Degree) eingestellt ist.
4)Wenn du den Tangenswert eines Winkels kennst und den Winkel berechnen willst, dann musst du die Umkehrfunktion des Tangens, naemlich den arctan, verwenden.
Beispiel 4: Berechne in deinem Heft den Winkel α wenn die Ankathete und die Gegenkathete 3 cm lang sind.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



