|
3.1 Zerlegung eines allgemeinen Dreiecks
|

 

|
Folgendes Dreieck wird mittels der Höhe h_c in zwei rechtwinkelige Dreiecke unterteilt:
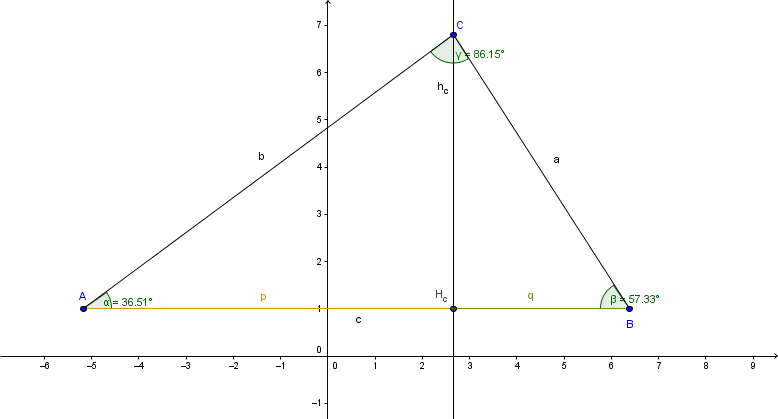
Dadurch können wir den bis jetzt erarbeiteten Stoff anwenden.
|
|
3.2 Herleitung Sinussatz
|

 

|
sin(α) = h_c : b ⇒ h_c = b ⋅ sin(α)
sin(β) = h_c : a ⇒ h_c = a ⋅ sin(β)
Wenn man jetzt die beiden Formeln für h_c gleich setzt bekomment man:
b ⋅ sin(α) = a ⋅ sin(β)
Und daraus erhält man nach einfachen Umformungen den Sinussatz:
b : sin(β) = a : sin(α)
Uebungsbeispiel
Wichtig: Werte für kurze Zeit, der Link öffnet sich oft nur langsam. Aktualisiere das Browserfenster des Links, wenn sich das Beispiel nicht von alleine öffnet!
|
|
3.3 Herleitung Kosinussatz
|

  
|
sin(α) = h_c : b ⇒ h_c = b ⋅ sin(α)
cos(α) = p : b ⇒ p = b ⋅ cos(α)
Damit lässt sich das Hilfsdreieck H_cBC:
Aus dem Satz von Pythagoras folgt:
a² = h_c² + (c - p)²
a² = b² ⋅ sin²(α) + (c - b ⋅ cos(α))²
a² = b² ⋅ sin²(α) + c² - 2bc ⋅ cos(α) + b² ⋅ cos²(α)
a² = b² ⋅ (sin²(α) + cos²(α)) + c² - 2bc ⋅ cos(α)
und wegen sin²(α) + cos²(α) = 1 erhält man:
a² = b² + c² - 2bc ⋅ cos(α)
Kreuzzahlenraetsel
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



