|
2.1 Was solltest du schon können?
|

 
|
Bevor du mit diesem Kapitel beginnst, solltest du bereits folgendes können:
Du weißt...
... dass der Differentialquotient als Grenzübergang (Δ x → 0) des Differenzenquotienten entsteht.
... wie man erste und höhere Ableitungen einer Polynomfunktion n-ten Grades bildet.
... wie man die erste und höhere Ableitungen von trogonometrischen und Exponentialfunktionen bildet.
... wie Produkt-, Quotienten- und Kettenregel angewandt werden.
Wiederholung, Lernstoff
|
|
2.4 Senkrechter Wurf
|

  
|
Beim senkrechten (=lotrechten) Wurf wird ein Gegenstand senkrecht nach oben geworfen oder fallengelassen. Die Weg-Zeit-Funktion des lotrechten Wurfes ist eine Parabel, also eine quadratische Funktion.
Das kannst du dir so vorstellen: Du und deine beste Freundin steht einander gegenüber. Du wirst einen Tennisball genau senkrecht nach oben, d.h. er sollte ohne, dass du dich bewegst, wieder bei dir landen. Deine Freundin notiert zu jeder Sekunde die Höhe des Balles (sie kann ziemlich gut schätzen). Zeichnet sie anschließend die Daten in ein Höhe-Zeit-Diagramm, wird sie näherungsweise eine Parabel erhalten. Das liegt an der Erdbeschleunigung g.
Beachte: Die Flugbahn des Tennisballes beschreibt KEINE Parabel, sondern er fliegt einfach gerade hinauf und wieder herunter.
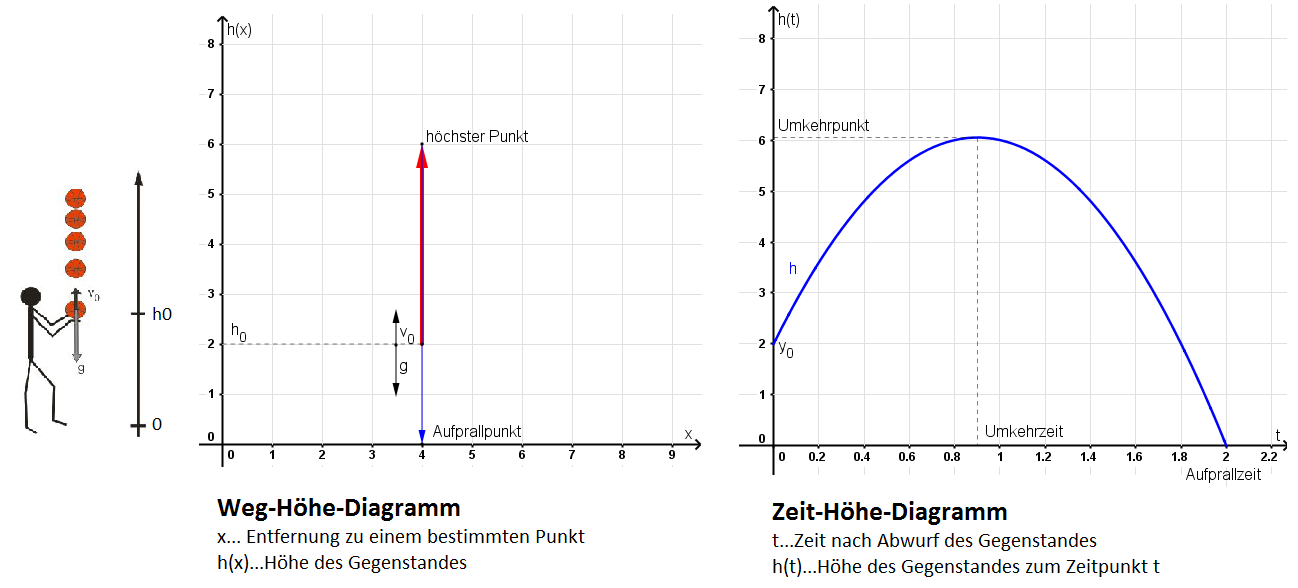
Diagramme zum senkrechten Wurf
(Quelle:Senkrechter Wurf)
Der lotrechte Wurf hat also im Allgemeinen die Form:
h(t) = h0 + v0 t - g/2 t2
h0 ... Abwurfhöhe
v0 ... Anfangsgeschwindigkeit, die der Werfer dem Gegenstand „mitgibt“
g ... Erdbeschleunigung, g ≈10 m/s2
Zusammenhang mit der Differentialrechnung:
Die physikalische Einheit der 1. Ableitung wird ja immer gebildet durch: Einheit der y-Achse/Einheit der x-Achse . Bei einem Weg-Zeit-Diagramm ist die Einheit der 1. Ableitung also m/s oder km/h.
Mithilfe der Differentialrechnung kann demnach durch die 1. Ableitung die Geschwindigkeit des senkrecht geworfenen Gegenstandes zu jeder Zeit (von Abwurf bis Aufprall) bestimmt werden. Die Beschleunigung erhält man durch zweifaches Ableiten der Höhe-Zeit-Funktion.
v(t) = h'(t) = v0 - gt
a(t) = h''(t) = -g
Die Geschwindigkeit zum Zeitpunkt t setzt sich zusammen aus der Anfangsgeschwindigkeit v0 und den durch die Erdbeschleunigung verursachten Anteil -gt.
Die Beschleunigung, die ja der zweiten Ableitung entspricht, ist bei einer Parabel konstant, also -g (d.h. die Krümmung hat überall den Wert -g).
Lernstoff
|
|
2.6 Aufgabe zum senkrechten Wurf 2
|

 

|
Kennst du die Legende, dass Newton ein Apfel auf den Kopf gefallen sein soll, wonach er das Gravitationsgesetz gefunden haben soll?

(Quelle: Newton und sein Apfel)
Wir nehmen an, der Apfel sei aus 3 Metern Höhe auf den schlafenden Isaac heruntergefallen. Die Anfangsgeschwindigkeit war in diesem Fall 0, da der Apfel ja nicht geworfen wurde.
a) Ermittle die Termdarstellung von h(t).
b) Mit welcher Geschwindigkeit fiel der Apfel Isaac auf den Kopf, wenn wir annehmen, dass sein Kopf in einer Höhe von 75 cm über dem Boden war?
c) Wie lang war der Apfel frei fallend, bevor er sein Ziel, Isaacs Kopf, erreichte?
d) Zeichne das Höhe-Zeit-Diagramm des Apfels für einen sinnvollen Zeitbereich.
Übungsaufgabe
|
|
2.11 Aufgaben zu Harmonischen Schwingungen 2
|

 

|
E(t)=5·sin(3t)
a) Zeichne die Funktion in dein Heft.
b) Leite die Funktion ab und skizziere die Ableitungsfunktion. Was sagt die 1. Ableitung aus?
c) Wie groß ist die Geschwindigkeit des Pendels an t=π/2, π, 4π/3
d) Wie groß ist die Beschleunigung des Pendels an t=π/2, π, 4π/3
Übungsaufgabe
|
2.12 Gedämpfte Schwingung - GeoGebra
https://ggbm.at/gPSs5N2r
|

 

|
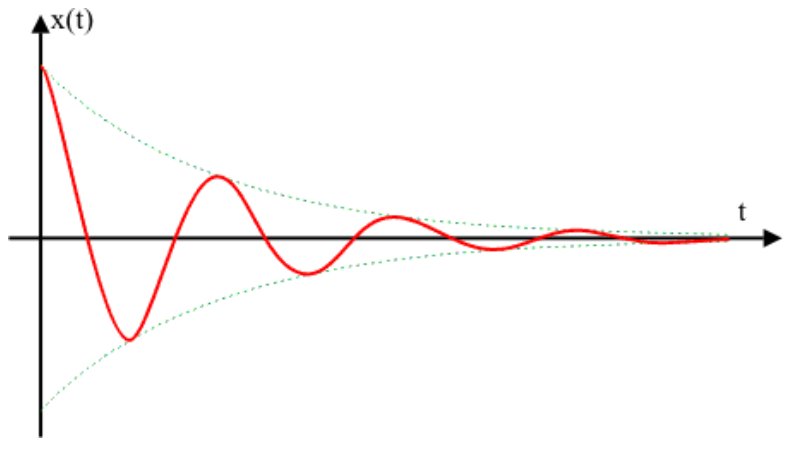
Gedämpfte mechanische Schwingung
Quelle: Leifi Physik
Im Alltag werden Schwingungen, denen nicht ständig Energie zugeführt wird, gedämpft. Grund dafür sind der Luftwiderstand oder Reibung in den Lagern. In diesem GeoGebra-File kannst du dir das Auslenkung-Zeit-Diagramm einer gedämpften Schwingung ansehen. Aufgabenstellungen findest du in der Datei.
Lernstoff, Übungsaufgabe, Vertiefung
|
|
2.14 Der Luftdruck
|

  
|
Der Luftdruck in unserer Atmosphäre nimmt exponentiell mit der Höhe ab. Wieder haben wir eine Änderung und können diesen Sachverhalt daher mit der Differentialrechnung behandeln. Die folgende Grafik zeigt dir den Höhenverlauf des Luftdruckes. Auf der x-Achse ist die Höhe in km aufgetragen, auf der y-Achse der Druck in hPa. Der Bodendruck beträgt 1013,25 hPa.
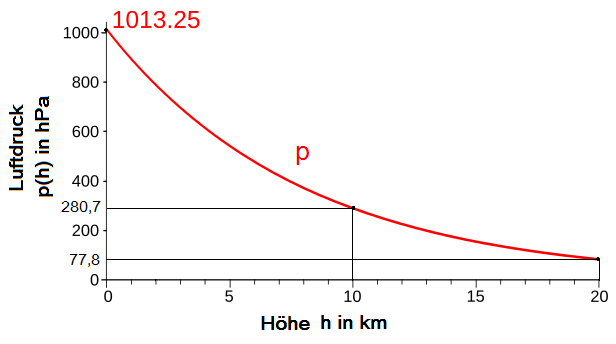
Druckabnahme in der Erdatmosphäre
(Quelle: Klaus-Dieter Keller - Eigenes Werk, CC BY-SA 3.0)
Zusammenhang mit der Differentialrechnung:
Da wir nun kein Weg-Zeit-Diagramm vorliegen haben, ist die Ableitung hier keine Geschwindigkeit. Da sich die physikalische Einheit der 1. Ableitung (wie in Abschnitt 2.2. beschrieben) wie folgt zusammensetzt Einheit der y-Achse/Einheit der x-Achse ist sie in diesem Fall: hPa/km (gesprochen: Hectopascal pro Kilometer). Für jede Höhe gibt der Differentialquotient also an, um wie viel Hectopascal der Luftdruck pro Kilometer Höhenänderung sinkt.
Lernstoff
|
|
2.15 Aufgaben zum Luftdruck
|

 

|
Löse die folgenden Aufgaben und notiere die Rechenschritte und Antworten in deinem Heft:
1.) Ermittle mithilfe der obigen Abbildung (in Abschnitt 2.8.) die Termdarstellung der Funktion p(h) in der Form p(h)=p0 · eλ·h.
2.) Bei welcher Höhe sinkt der Luftdruck auf unter 1% seines Bodenwertes?
3.) Leite die Funktion ab und berechne den Druckabfall pro Kilometer für h=0,5,10,30 km.
4.) Bei welcher Höhe beträgt der Druckabfall pro Kilometer -70 hPa/km?
Übungsaufgaben
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



