|
1.1 Winkelzeichnen und Winkelmessen
|
|
Zuerst wiederholen wir den Unterstufenstoff.
Dazu öffne bitte das Übungsblatt und bearbeitet die Aufgaben.
Du findest auch Lösungen zum Übungsblatt. Bitte öffne diese erst, wenn du dir sicher bist, dass du mit dem Übungsblatt fertig bist.
Übungsblatt
Lösungen zum Übungsblatt
Bitte trage die Merksätze in dein Lerntagebuch ein.
Merke:
Die Innenwinkelsumme im Dreieck beträgt 180°.
Hier kannst du testen, wie gut du den bisherigen Stoff beherrscht:
Selbsttestung
Lernstoff, Eintrag in das Lerntagebuch, Wiederholung
|
|
1.2 Einführung des Tangens
|
|
Beispiel:
Eine Leiter steht 2m von einer Mauer entfernt. Der Boden und die Leiter schließen einen Winkel von 60° ein.
Wie hoch reicht die Leiter an der Mauer hinauf?
Zeichne die Situation in einem geeignetem Maßstab und entnimm das Ergebnis zuerst aus deiner Zeichnung.
Versuche es dann rechnerisch zu lösen.
Lösung zum Beispiel
Bitte trage die Merksätze in dein Lerntagebuch ein.
Merke:
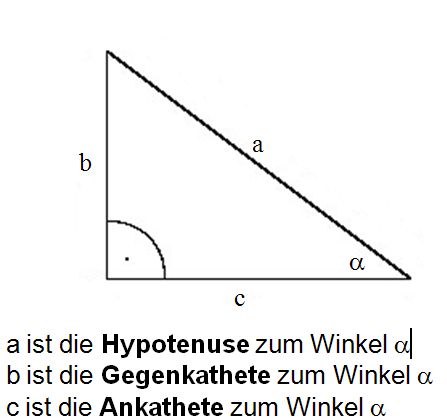
Tangens(a) = Länge der Gegenkathete / Länge der Ankathete
Dies gilt nur im rechtwinkeligen Dreieck.
weiteres Beispiel zum Tangens
Lösung zum weiteren Beispiel
Lernstoff, Eintrag in das Lerntagebuch
|
|
1.4 Einführung in den Cosinus
|
|
Beispiel:
Eine 4m hohe Leiter ist an einer Mauer angelehnt.
Der Boden und die Leiter schließen einen Winkel von 60° ein.
Wie weit steht die Leiter am Boden von der Mauer entfernt?
Zeichne die Situation in einem geeignetem Maßstab und entnimm das Ergebnis zuerst aus deiner Zeichnung.
Versuche es dann mit den bisher gelernten Methoden rechnerisch zu lösen.
Lösung zum Beispiel
Bitte trage die Merksätze in dein Lerntagebuch ein.
Merke:
Cosinus(a) = Länge der Ankathete / Länge der Hypotenuse
Dies gilt nur im rechtwinkeligen Dreieck.
vermischte Aufgaben zu Sinus, Cosinus und Tangens
Lösungen zu den vermischten Aufgaben
Lernstoff, Eintrag in das Lerntagebuch
|
|
1.6 Einführung in den Arcustangens, Arcussinus und Arcuscosinus
|
|
Bei manchen Beispielen will man nicht die Länge von Strecken ausrechnen, sondern die Winkel.
Dafür gibt es die Arcusfunktionen.
Übungsblatt zu den Arcusfunktionen
Lösungen zum Übungsblatt
Bitte trage die Merksätze in dein Lerntagebuch ein.
Merke:
a = Arcustangens (Länge der Gegenkathete/ Länge der Ankathete)
a = Arcussinus (Länge der Gegenkathete / Länge der Hypotenuse)
a = Arcuscosinus (Länge der Ankathete / Länge der Hypotenuse)
Dies gilt nur im rechtwinkeligen Dreieck.
Hier kannst du überprüfen, ob du das bisher Gelernt verstanden hast:
Selbsttestung
Lernstoff, Eintrag in das Lerntagebuch
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|
