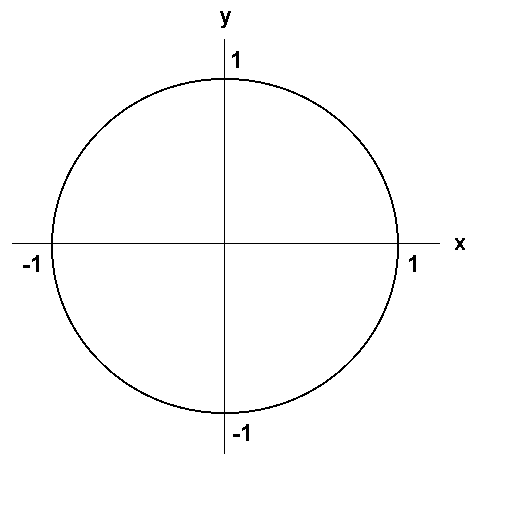
Der Einheitskreis ist ein Kreis, dessen Mittelpunkt im Koordinatenursprung liegt und dessen Radius gleich 1 ist.

Bisher kennen wir die Winkelfunktionen nur im rechtwinkeligen Dreieck. 
Am Einheitskreis kann man sehen, dass Tangens, Sinus und Cosinus auch für Winkel größer 90° sinnvoll sind. 
Versuche bei dem Link auf eine Geogebra-Seite dir den Sinus, Cosinus und Tanges am Einheitskreis genau anzuschauen. 

Beziehungen am Einheitskreis in Geogebra

Überlege dir zuerst die Ergebnisse der Tabelle und überprüfe dann auf deinem Taschenrechner.
(Achtung: Der Taschenrechner muss auf Degree eingestellt sein)


  

    

sin(0°)=
sin(90°)=
sin(180°)=
sin(270°)=
sin(360°)=
    

    

cos(0°)=
cos(90°)=
cos(180°)=
cos(270°)=
cos(360°)=
    

    

tan(0°)=
tan(90°)=
tan(180°)=
tan(270°)=
tan(360°)=
    

  



Danach schau, dir die folgenden Beziehungen an und versuche sie anhand des Einheitskreise zu verstehen.
Überprüfe die Beziehungen auch am Taschenrechner.
Tipp:
Suche dir einen Winkel aus (z.B. a=20°) und setze diesen immer für a ein, so kannst du die Beziehungen besser erkennen. 


  

    

sin(a) = sin(180°-a)
sin(a) = -sin(180°+a)
sin(a) = -sin(360°-a)
sin(a) = -sin(-a)
    

    

cos(a) = -cos(180°-a)
cos(a) = -cos(180+a)
cos(a) = cos(360°-a)
cos(a) = cos(-a) 
    

    

tan(a) = -tan(180°-a)
tan(a) = tan(180°+a)
tan(a) = -tan(360°-a)
tan(a) = -tan(-a)
    

  



Notiere dir die Ergebnisse aus der ersten Tabelle und die für dich wichtigesten Beziehungen in deinem Lerntagebuch.


Hier kannst du testen, wie gut du den bisherigen Stoff beherrscht: 
Selbsttestung