|
2.1 Mittelpunktsgleichung des Kreises
|

  
|
Der Kreis ist die Menge aller Punkte, die von einem Mittelpunkt M den selben Abstand haben. Also in der Sprache der Mathematik formuliert:
k = {X | XM = r}
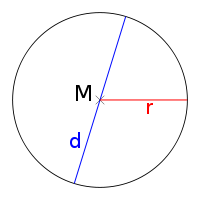
M: Mittelpunkt
r: Radius
d: Durchmesser (d = 2r)
Für einen Kreis, dessen Mittelpunkt im Koordinatenursprung (1. Hauptlage) liegt und die Koordinaten eines Punktes X(x|y), der auf dem Kreis liegt, gilt folgende Formel:
x2 + y2 = r2
Ansonsten gilt für den Mittelpunkt M(xM|yM) die allgemeine Formel
(x - xM)2 + (y - yM)2 = r2
AUFGABE 2.1
Löse mindestens jeweils zwei der folgenden Aufgaben im Schulübungsheft.
a) Ermittle die Gleichung der Kreise:
1. M(3/2), r = 5
2. M(-2/4), r = 3
3. M(3/-1), r = √10
4. M(-2/-2), P(5/1) auf k
5. M(5/10), P(3/7) auf k
6. M(4/2), k berührt y-Achse
7. M(5/-3), k berührt x-Achse
8. M(-3/-4), O(0/0) auf k
b) Berechne Mittelpunkt und Radius der folgenden Kreise:
1. k: x² + y² - 4x - 8y + 4 = 0
2. k: x² + y² - 10x + 6y - 2 = 0
3. k: x² + y² + 10x - 2y - 10 = 0
4. k: x² + y² + 6x - 16 = 0
5. k: x² + y² - 12y + 20 = 0
6. k: 3x² + 3y² - 60y + 57 = 0
7. k: x² + y² - 5x + 10y = 0
8. k: x² + y² - 3x - 5y - 4 = 0
Hilfreiche Tipps und Beispiele findest du unter diesem Link
Lernstoff
|
|
2.2 Mittelpunktsgleichung der Ellipse
|

  
|
Die Ellipse besteht aus allen Punkten X, für die die Summe der Abstände von zwei festen Punkten - den Brennpunkten F1 und F2 - konstant ist. Mathematisch formuliert lautet die Definition folgendermaßen:
ell = {X | XF1 + XF2 = 2a}
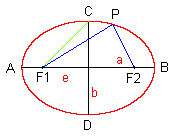
A, B: Hauptscheitel
C, D: Nebenscheitel
F1, F2: Brennpunkte
2a: Hauptachse
2b: Nebenachse
e: Brennweite (lineare Exzentrizität)
Normalerweise wird (zumindest in der Schule) vorausgesetzt, dass die Ellipse entweder in
1. Hauptlage: Mittelpunkt im Koordinatenursprung, Hauptachse auf der x-Achse, oder in
2. Hauptlage: Mittelpunkt im Koordinatenursprung, Hauptachse auf der y-Achse, liegt.
Die Ellipsengleichung für die Koordinaten des Punktes X(x|y) lautet in 1. Hauptlage:
x2/a2 + y2/b2=1
(in 2. Hauptlage: x2/b2 + y2/a2=1)
Außerdem lässt sich die Exzentrizität e wie folgt berechnen:
e2 = a2 - b2
AUFGABE 2.2
Wie lauten die Gleichungen der folgenden Kegelschnitte in 1. Hauptlage? (Ohne Brüche! Löse mindestens zwei der Aufgaben im Schulübungsheft.)
a) ell: a = 5, b = 3
b) ell: a = 20, b = 5
c) ell: a = 10, e = 8
d) ell: a = 4, e = 2√2
e) ell: b = 5, e = 10
f) ell: b = 10, e = 5√5
Lernstoff
|
|
2.3 Mittelpunktsgleichung der Hyperbel
|

  
|
Die Hyperbel besteht aus allen Punkten, für die die Differenz der Abstände von den Brennpunkten konstant ist. Mathematisch ausgedrückt:
hyp = {X | |XF1 - XF2| = 2a}
Sie besteht aus zwei Ästen und besitzt zwei Asymptoten u und v.

A, B: Hauptscheitel
C, D: Nebenscheitel
F1, F2: Brennpunkte
2a: Hauptachse
2b: Nebenachse
e: Brennweite (lineare Exzentrizität)
u, v: Asymptoten
Bei einer gleichseitigen Hyperbel ist a = b.
1. und 2. Hauptlage definiert man wie bei der Ellipse.
Die Hyperbelgleichung für die Koordinaten des Punktes X(x|y) lautet in 1. Hauptlage:
x2/a2 - y2/b2=1
(in 2. Hauptlage: -x2/b2 + y2/a2=1)
Außerdem ist die Gleichung der Asymptoten(in 1. Hauptlage):
y = ±xb/a
AUFGABE 2.3
Wie lauten die Gleichungen der folgenden Kegelschnitte in 1. Hauptlage? (Ohne Brüche! Löse mindestens zwei der Aufgaben im Schulübungsheft.)
a) hyp: a = 3, b = 4
b) hyp: a = 5, b = 5
c) hyp: a = 4, e = 5
d) hyp: a = 4, e = 6
e) hyp: b = 8, e = 10
f) hyp: b = 3√3, e = 9
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



