Die einfachste und schnellste Methode, eine Ellipse auf dem Papier zu konstruieren ist die Konstruktion mit Hilfe der sogenannten Schmiegekreise.
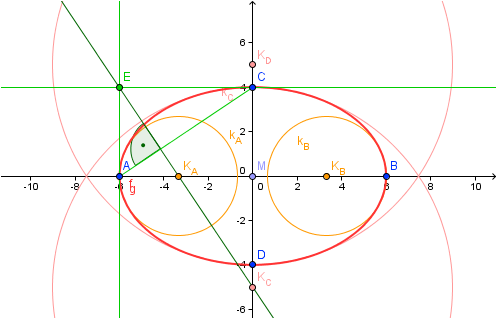
1. Man verbindet die Scheitel A und C und zeichnet die Parallelen zu h und n in C bzw. A, ihr Schnittpunkt heißt E.
2. Man zeichnet die Normale zu AC durch E.
3. Der Schnittpunkt KA von der Normalen durch E und h ist der Mittelpunkt des Krümmungskreises kA im Scheitel A.
Für den Krümmungskreisradius rA gilt: rA = b2 / a
4. Der Schnittpunkt KC von der Normalen durch E und n ist der Mittelpunkt des Krümmungskreises kC im Scheitel C.
Für den Krümmungskreisradius rC gilt: rC = a2 / b
5. Die Mittelpunkte der Schmiegekreise an den Achsen spiegeln und die Ellipse einzeichnen.
Falls dir das jetzt etwas zu schnell gegangen ist, kannst du die einzelnen Schritte noch einmal auf dieser Powerpointpräsentation ansehen: Wie zeichne ich eine Ellipse?
Eine weitere Konstruktionsmöglichkeit siehst du, wenn du dir das Video unter folgendem Link ansiehst:
Ellipsenkonstruktion mit dem Faden
AUFGABE 3.1
a) Welche Eigenschaften der Ellipse macht man sich mit der Gärtnerkonstruktion (siehe Video oben) zunutze? Erkläre, warum es funktioniert (-> Schulübungsheft)
b) Konstruiere eine Ellipse in deinem Schulübungsheft (wähle geeignete Maße).
Lernstoff
|



