|
2.1 Was ist eine Wurzel?
|

 
|
Auch mit Wurzeln hast du in der Schule schon viel gerechnet. Aber weißt du auch, wie eine (Quadrat-)Wurzel definiert wird? Versuche eine exakte mathematische Definition zu finden.
Vielleicht helfen dir die folgenden Überlegungen:
Eine Wurzel kann man ja, wie du weißt, als Potenz mit einer Bruchzahl als Exponent darstellen. Ist es daher möglich, die Definition von Potenzen einfach auszudehnen und rationale Zahlen als Exponenten zuzulassen? Warum ist das nicht ganz so einfach?
Überleg nochmal genau, was es eigentlich bedeutet aus einer Zahl eine Wurzel zu ziehen: Man sucht eine Zahl, die ...?
|
|
2.2 Definition Wurzel
|

 
|
Hier die exakte mathematische Definition:
Die n-te Wurzel aus einer nichtnegativen Zahl a ist jene nichtnegative Zahl b, deren n-te Potenz gleich a ist.
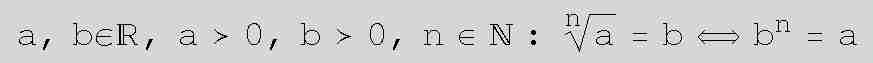
Dabei nennt man a Radikand, n Wurzelexponent und b Wurzel.
|
|
2.3 Zusammenhang Wurzel - Potenz
|

 
|
Wenn man obige Definition hernimmt, erkennt man, dass es einen Zusammenhang zwischen Wurzeln und Potenzen gibt. Um diesen Zusammenhang offensichtlicher zu machen, wird folgende Definition eingeführt (Achtung, kein Satz!):

Dadurch können wir nun die Definition von Potenzen auf Potenzen mit rationalen Exponenten ausdehnen:
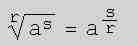
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



