3.1 Was ist ein Logarithmus?
http://www.mathe-online.at/mathint/log/i.html#Logarithmus
|

 
 
|
Versuche zunächst, folgende Fragen zu beantworten:
- Bei welchen Aufgaben hast du in der Schule den Logarithmus gebraucht? (Nicht unbedingt die Logarithmusfunktion, sondern einfach den Logarithmus als Rechenoperation)
- Löse die Aufgabe für x: 2x=8. Obwohl du diese Aufgabe wahrscheinlich im Kopf lösen kannst - was hat sie mit dem Logarithmus zu tun? Wie würdest du z.B. 2x=7 lösen?
- Worin besteht also der Zusammenhang zwischen Potenzen und Logarithmus?
- Versuche nun, eine Definition für den Logarithmus zu finden!
Klicke nun auf obigem Link und lies dir das Kapitel "Logarithmus" (Logarithmusfunktionen nicht mehr) genau durch. Überleg dir genau, was die Definition des Logarithmus bedeutet und vergleiche sie mit deiner Definition.
|
|
3.2 Definition Logarithmus
|

 
|
Hier nochmal zusammenfassend die Definition des Logarithmus. Versuche, sie dir einzuprägen und überleg genau, was mit damit gemeint ist:

Zur Erklärung:
Jede Zahl b kann man als Potenz einer beliebigen Zahl a darstellen. Man muss nur das richtige x finden. Beim Zusammenfassen von verschiedenen Termen kann diese Erkenntnis sehr nützlich sein. Das Problem besteht nun darin, das richtige x zu finden, was der Logarithmus für dich übernimmt: Ziehe einfach den Logarithmus von b zur Basis a und du hast die gesuchte Zahl x! Meist brauchst du zur Ausführung dieser Aufgabe jedoch den Taschenrechner.
|
|
3.3 Rechenregeln
|

 
|
Auch zum Rechnen mit Logarithmen gibt es Rechenregeln, die sich von den Rechenregeln für Potenzen und der Definition des Logarithmus ableiten:

Wenn du Lust hast, kannst du wieder versuchen, diese Rechenregeln zu beweisen. Es wird dir helfen, den Logarithmus genauer zu verstehen und du kannst dir dann die Regeln auch leichter merken.
Hier findest du die Beweise der ersten beiden Regeln, und hier die Beweise der anderen beiden Regeln.
|
|
3.4 Umrechnen von Basen
|

 
|
Da wir eine Zahl b als Potenz eine beliebigen Zahl (Basis) ausdrücken können, ist es auch möglich die Basis zu wechseln. Die Regeln zur Umrechnung einer Basis in eine andere kannst du dir hier durchlesen (bis "Logarithmus am Computer").
Klicke unter obigem Link auch rechts auf "Beweise" um genauer zu verstehen, warum diese Umrechnungsregel gilt.
Da man oft den natürtlichen Logarithmus zur Basis e (Eulersche Zahl = 2.718...) verwendet. Daher hier nocheinmal die Umrechnungsregel eingesetzt um vom natürlichen Logarithmus zu einer anderen Basis zu kommen:
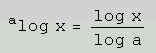
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



