|
1.1 Einleitung
|

 
|
Dieses erste Kapitel besteht zum größten Teil aus Wiederholungen von bereits gelernten Themen, wie an der Kennzeichnung der entsprechenden Abschnitte ersichtlich ist.
Wenn du der Meinung bist, dass du die jeweiligen Inhalte bereits beherrschst, kannst du sie also gerne überspringen.
|
|
1.2 DER KREIS: Radius, Umfang und Bogenlänge
|

 
|
Mathematische Definition
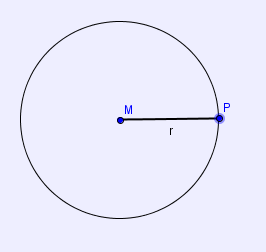
Der Kreis ist die Menge aller Punkte P, die von einem festen Punkt M immer denselben Abstand r haben.
Der Punkt M wird Mittelpunkt des Kreises mit dem Radius r genannt.
Umfang des Kreises
Um den Umfang, also die Länge der Kreislinie zu berechnen benötigt man die sogenannte Kreiszahl Pi: π = 3,14159...
Sie ist für jeden beliebigen Kreis der Quotient aus dem Umfang und dem Durchmesser (2·r), wodurch sich die folgende Formel ergibt:
U = 2·r·π
Länge eines Kreisbogens
Mithilfe der obigen Formel lässt sich die Länge der gesamten Kreislinie berechnen.
Der Kreisbogen b ist ein Teil davon und hängt vom Mittelpunktswinkel α ab, was man sehr schön am Bild unten erkennen kann.

Bei einem Winkel von α=360° entspricht der Kreisbogen dem Umfang des Kreises (U = 2·r·π), woraus sich der Kreisbogen mit Mittelpunktswinkel α=1° wie folgt ergibt:
α=1° 2·r·π und somit für beliebige Winkel: α=x° 2·r·π
b = ----- b = ----- · x
360 360
Nun kann man noch kürzen und erhält damit die Formel für die
Länge des Kreisbogens b mit dem Mittelpunktswinkel α:
r·π
b = ---- · α
180
Wiederholung
|
|
1.3 Eine andere Art, Winkel anzugeben
|

 

|
Passend zum vorherigen Thema folgt nun ein kleiner Vorgriff auf den Stoff der 6. Klasse AHS, der notwendig ist, um den Inhalten des Lernpfades zu folgen.
Das Bogenmaß
Neben dem bekannten "Gradmaß" kann man Winkel auch mit dem sogenannten "Bogenmaß" angeben.
Es ist definiert als das Verhältnis der Bogenlänge mit dem Radius eines Kreises und hat die Einheit "Radiant"
b
α = --- ; [b/r] = rad
r
In einem Kreis mit Radius r=1 entspricht also die Bogenlänge des Kreissektors dem Mittelpunktswinkel im Bogenmaß und du kannst dir folgende Zusammenhänge ganz einfach selbst überlegen:
α = 90° —► α = π/2 rad
α = 180° —► α = π rad
α = 270° —► α = 3·π/2 rad
α = 360° —► α = 2·π rad
Vorgriff
|
|
1.5 TRIGONOMETRIE: Winkelfunktionen am rechtwinkeligen Dreieck
|

 
|
Die trigonometrischen Funktionen: Sinus, Cosinus und Tangens
Per Definition sind die trigonometrischen Funktionen (auch Winkelfunktionen genannt) rechnerische Zusammenhänge zwischen Winkeln und Verhältnissen von Seiten im rechtwinkeligen Dreieck
und es gilt für 0 ≤ φ < 90°:
Gegenkathete Ankathete Gegenkathete
sin(φ) = ------------ cos(φ) = ----------- tan(φ) = -------------
Hypotenuse Hypotenuse Ankathete
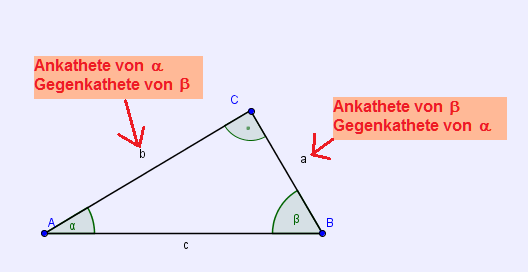
Überlege dir nun, wie die Winkelfunktionen im obigen Dreieck für α und β definiert sind und vergleiche deine Ergebnisse danach mit der Lösung unten.
Lösung [Markiere den folgenen Text, um ihn lesen zu können]
sin(α) = a/c
cos(α) = b/c
tan(α) = a/b
sin(β) = b/c
cos(β) = a/c
tan(β) = b/a
Ende der Lösung
Wiederholung
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



