|
3.1 Einleitung
|

 
|
Neben der Periodizitätseigenschaft der Winkelfunktionen gibt es noch einige weitere Beziehungen, die nun in diesem Kapitel behandelt werden.
|
|
3.2 Verschiedene Überlegungen am Einheitskreis
|

 

|
Es folgen nun einige "Regeln", die die Arbeit mit trigonometrischen Funktionen erleichtern. Versuche nicht nur die Regeln auswendig zu lernen sondern auch deren "Herleitungen" zu verstehen und nachzuvollziehen!
1) Der Lehrsatz des Pythagoras im Einheitskreis
Hierbei handelt es sich um eine der nützlichsten Beziehungen, wenn man mit Winkelfunktionen rechnet.
Betrachte eines der rechtwinkeligen Dreiecks, das du einem der Quadranten des Einheitskreises eingeschrieben hast, und wende nun den Lehrsatz des Pythagoras darauf an, um folgende Beziehung zu erhalten:
sin²(α) + cos²(α) = 1 für beliebige Winkel α
Hinweis: Dass die Regel nicht nur für die rechtwinkeligen Dreiecke sondern auch an den "kritischen" Stellen (Kapitel 2) gilt, kannst du dir selbst überlegen.
2) sin(α) = sin(β) oder sin(α) = -sin(β) (und analog für cos und tan)
Es werden nun zwei verschiedene Winkel gesucht, deren Beträge der Sinuswerte genau ident sind. Im vorigen Kapitel haben wir bereits eine mögliche allgemeine Lösung gefunden, die sich der Periodizitätseigenschaft der Winkelfunktionen bedient. Nun wollen wir aber auch nach Lösungen im Bereich 0°-360° suchen. Dass es mehrere gibt, ist naheliegend, da der Sinus beim Durchgang durch alle 4 Quadranten mehrmals anwächst und schrumpft.
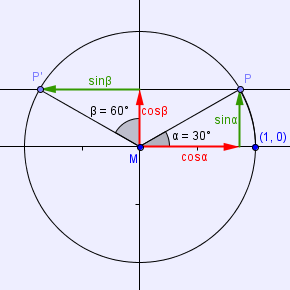
a) sin(α) = sin(β) - Betrachte die folgende Figur:
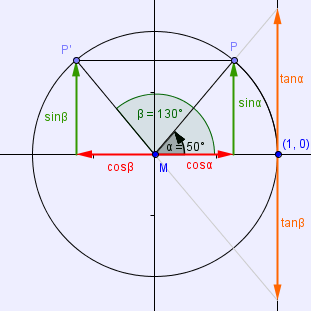
Der Punkt P' ist die Spiegelung des Punktes P an der y-Achse, also gilt in diesem Fall tatsächlich: sin(α) = sin(β), werfen wir also einen Blick auf die Winkelangaben:
Ihre Summe beträgt genau 180°, was man auch sehr gut anhand der Zeichnung erkennen kann.
Würde man P nun bewegen, würden sich beide Winkel so verändern, dass sie trotzdem noch zusammen 180° ergeben, wie in der Grafik unten ersichtlich ist:
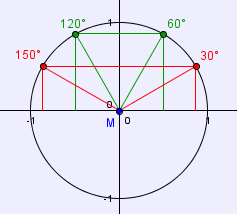
Für beliebige Winkel α gilt demnach: sin(α) = sin(180°-α) bzw.(im Bogenmaß) sin(α) = sin(π-α)
Dieselbe Winkelbeziehung gilt auch für cos(α) und tan(α) mit dem einzigen Unterschied, dass sich die Werte im Vorzeichen unterscheiden:
cos(α) = -cos(180°-α)
tan(α) = -tan(π-α)
Damit haben wir eine Beziehung gefunden; es gibt aber noch weitere:
b) cos(α) = cos(β)
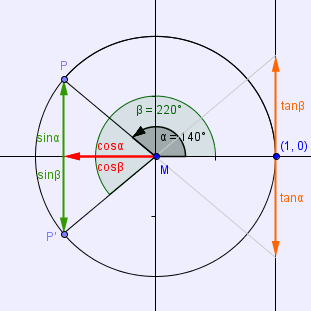
Die Winkelsumme von α und β ist nun 360° und es gilt somit:
sin(α) = -sin(360°-α) bzw.(im Bogenmaß) sin(α) = -sin(2·π-α)
cos(α) = cos(360°-α)
tan(α) = -tan(360°-α)
c) tan(α) = tan(β)
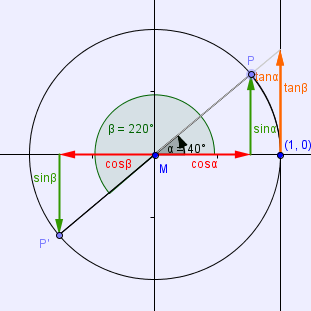
In diesem Fall ergibt nun die Differenz der Winkel 180°. Um also β zu erhalten, muss man α zu den 180° hinzuaddieren:
sin(α) = -sin(180°+α) bzw.(im Bogenmaß) sin(α) = -sin(π+α)
cos(α) = cos(180°+α)
tan(α) = -tan(180°+α)
3) sin(α) = cos(β) (und umgekehrt)
Um die folgende Beziehung zu verstehen, musst du zunächst etwas abstrakter denken:
Stelle dir zwei Einheitkreise mit selbem Mittelpunkt vor, wobei einer davon um 90° verdeht ist - in etwa so wie im Bild unten:
Das Dreieck mit Mittelpunktswinkel α liegt dabei im 1. Quadranten des gewöhnlichen Einheitskreises. Das andere Dreieck hingegen liegt im 1. Quadranten des um 90° verdehten Einheitskreises, wodurch der sin(β) ebenso POSITIV ist, obwohl der Pfeil nach links zeigt.
Damit solltest du nun die folgenden beiden Beziehungen nachvollziehen können:
sin(α) = cos(90°-α) bzw.(im Bogenmaß) sin(α) = cos(π/2)
cos(α) = sin(90°-α)
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



