|
2.1 Einleitung
|

 

|
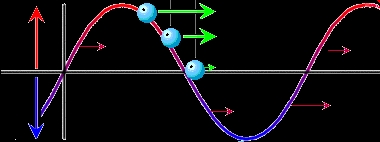
Im oberen Bild (Quelle) sehen wir ein Elektron (hellblaues Teilchen), das sich entlang einer Welle in einem Koordinatensystem bewegt. Weiters wird die Welle durch die Funktion f(x)=sin(x) beschrieben.
Stellen wir uns nun vor, dass das Teilchen immer auf der x-Achse stehen bleibt, wenn es diese überqueren will.
Ist dies der Fall, so befindet sich das Teilchen genau auf der Nullstelle der Welle, wobei x=0 und der Funktionswert f(x) ein ganzzahliges Vielfaches von π ist.
Da eine sinusförmige Welle fortlaufend ist, bedeutet dies, dass hier unendlich viele Nullstellen vorhanden sind.
|
|
2.2 Nullstellen
|

  
|
Im folgenden Text findest du einige Informationen über Nullstellen. Bitte lies ihn dir aufmerksam durch, denn du wirst ihn in den folgenden Kapiteln brauchen. Außerdem ist es sinnvoll dir die wichtigsten Punkte in deiner Mitschrift zu notieren.
Text
|
|
2.3 Graphische Darstellung
|

  
|
Damit wir uns das Verhalten von Nullstellen auch graphisch vorstellen können,
ist hier ein Link. Überlege dir auch, ob du jemanden die Graphik erklären kannst.
|
|
2.4 Aufgaben
|

 

|
Hier kannst und sollst du dein erlerntes Wissen nochmals anwenden und überprüfen. Berechne also die Nullstellen und zeichne die Graphen der Funktionen.
• f(x)= x²+5x-10
• g(x)= x³-4x²+0.5x-1
Lösungen
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



