|
1.2 Beispiele
|

 

|
1) Zeichne den Vektor (-2,1) drei Mal in das Koordinatensystem ein. Verwende dabei immer einen anderen Anfangspunkt.
2) Gegeben sind die folgenden Punkte: M=(4,7) und N=(1,-3).
Berechne den Vektor 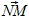 rechnerisch und grafisch. rechnerisch und grafisch.
3) Gegeben ist der Punkt T = (5,5) und der Vektor 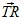 = (-1,2). = (-1,2).
Berechne den Endpunkt R und zeichne ein Koordinatensystem, dass die Punkte und den Vektor enthält.
Übungsaufgaben, Rechnen im Schulübungsheft
|
|
1.5 Beispiele
|

 

|
1) Berechne den Abstand der Punkte P = (-3,2) und Q = (1,5). Fertige auch eine Zeichnung an!
2) a. Berechne den Abstand der Punkte U = (-1,1) und V = (3,-1).
b. Fertige eine Zeichnung an.
c. Berechne die Normalvektoren zum Vektor 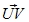 . .
3) Berechne die Längen der Seiten des Dreiecks ABC mit A = (-1,-1), B = (-5,2), C = (7,7) und fertige eine Zeichnung an.
Übungsaufgaben, Rechnen im Schulübungsheft
|
|
1.6 Vektorenquiz
|

 

|
Hast du alles verstanden?
Hier kannst du dein Wissen überprüfen:
Vektorenquiz
Selfchecking Test
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



