Die Multiplikation eines Vektors mit einer reellen Zahl
Eine Erklärung anhand eines Beispieles:
Es ist ein Vektor 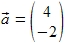 gegeben. gegeben.
Nun wollen wir ihn mit 0,5 multiplizieren:

Betrachten wir die Multiplikation eines Vektors mit einer reellen Zahl in einer Grafik:

Sei 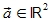 und
und 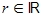 .
.
Werden die Vektoren 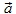 und
und 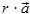 durch Pfeile in der Ebene dargestellt, dann gilt:
durch Pfeile in der Ebene dargestellt, dann gilt:
1. Der zu 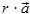 gehörige Pfeil hat die |r| -fache Länge des zu
gehörige Pfeil hat die |r| -fache Länge des zu 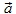 gehörigen Pfeiles.
gehörigen Pfeiles.
2. Ist 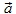 ≠ 0, dann sind die beiden Pfeile gleichsinnig parallel, falls r > 0, und ungleichsinnig parallel, falls r < 0.
≠ 0, dann sind die beiden Pfeile gleichsinnig parallel, falls r > 0, und ungleichsinnig parallel, falls r < 0.
Lernstoff
|



