|
2.1 Einleitung
|

 

|
Erarbeite die Reglen fuer das Addieren und Subtrahieren von Vektoren mit zwei
Komponenten sowie die Multipliation eines Vektors mit einer reellen Zahl erarbeiten.
Die drei folgenden Definitionen der Rechenoperationen Addition, Subtraktion und Multiplikation mit einer reellen Zahl gelten fuer beliebige Vektoren mit n Komponenten.
�bungsaufgabe, Wiederholung
|
|
2.2 Addition
|

  
|
Definition:
Vekoren werden addiert, indem komponentenweise die Summe gebildet wird.
Fuer Vektoren mit drei Komponenten gilt:
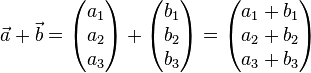
Uebung:
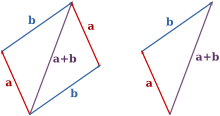
Bei dem folgenden Beispiel (oeffne dazu den Link), siehst du in der Zeichnung die Vektoren
a, b und c, die durch drei Pfeile repraesentiert werden
. Finde heraus, welche Bedeutung der Pfeil c
in Zusammenhang mit a und b hat.
Uebungsbeispiel Addition
Lernstoff
|
|
2.3 Subtraktion
|

  
|
Definition:
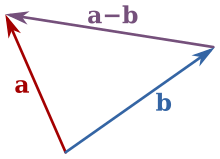
Vektoren werden subtrahiert, indem komponentenweise die Differenz gebildet wird.
Fuer Vektoren mit drei Komponenten gilt:

Uebung:
Bei dem folgenden Uebungsbeispiel, siehst du in der Zeichnung die Vektoren a, b und c, die durch drei Pfeile repräsentiert werden. Finde heraus, welche Bedeutung der Pfeil c in Zusammenhang mit a und b hat.
Uebung Subtrahieren
Lernstoff
|
|
2.4 Uebungsblatt: Addition und Subtraktion von Vektoren
|

 

|
Loese das Beispiel zur Addition und Subtraktion von Vektoren
Uebungsblatt
�bungsaufgabe
|
|
2.5 Multiplikation
|

 
|
Definition:
Vektoren werden mit einer reellen Zahl multipliziert, indem jede Komponente des Vektors
mit der Zahl multipliziert wird.
Das Ergebnis ist ein Vielfaches der urspruenglichen Vektors.
Fuer Vektoren mit drei Komponenten gilt:
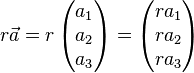

Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



