|
3.1 Einleitung
|

 
|

Nachdem du die vorhergehenden Kapitel nun hoffentlich gut verinnerlicht hast, kommen wir nun zum Hauptkapitel dieses Lernpfads.
In den folgenden Punkten wird dir zuerst die Herleitung der Winkelfunktionen im Einheitskreis präsentiert und im Anschluss gezeigt,
wie du dieses Wissen außerdem gut einsetzen kannst.
|
|
3.2 Konstruktion der Winkelfunktionen im 1. Quadranten des Einheitskreises
|

  
|
Schon im vorhergehenden Kapitel haben wir den Einheitskreis erwähnt. Es handelt sich hierbei um einen Kreis, dessen Radius r = 1 ist.
Die 1 steht hierbei naturgemäß für "eine Einheit" und kann z.B. als 1 cm, 1 m, etc. bezeichnet werden.
Wie so oft benötigt man diese 1, um aus vorhandenen Formeln neue Erkenntnisse abzuleiten.
Zuerst müssen wir den Begriff "Quadrant" klären.
Wenn wir einen Einheitskreis mit Radius r = 1 und Mittelpunkt M = (0/0) zeichnen, erstreckt sich dieser über alle 4 Abschnitte des Koordinatensystems.
Diese Abschnitte werden "Quadranten" genannt und IMMER in der Reihenfolge von 1 - 4 benannt, wie es unten (in Abb. 4) zu sehen ist.
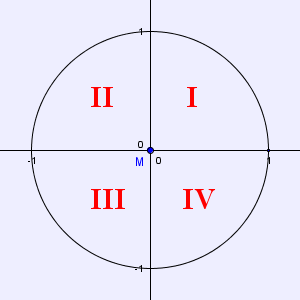
Abb. 4 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
Wenn wir nun im 1. Quadranten einen beliebigen Punkt P auf der Kreislinie bestimmen, ergibt sich daraus ein rechtwinkeliges Dreieck, wie unten (in Abb. 5) abgebildet.
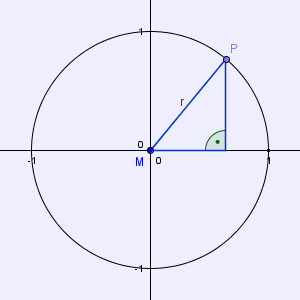
Abb. 5 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
Da der Kreis den Radius r = 1 hat, ist die Hypotenuse des Dreiecks eben genau eine Einheit lang.
Nun folgt aus den uns bereits bekannten trigonometrischen Funktionen im rechtwinkeligen Dreieck:
Gegenkathete Gegenkathete
sin(φ) = - - - - - - - - - - - - = - - - - - - - - - - - - = Gegenkathete
Hypotenuse 1
Ankathete Ankathete
cos(φ) = - - - - - - - - - - = - - - - - - - - - - = Ankathete
Hypotenuse 1
Wenn wir nun also sin(φ) mit der Gegenkathete und cos(φ) mit der Ankathete auch im Einheitskreis gleichsetzen, erhalten wir das gewünschte Bild (siehe Abb. 6).
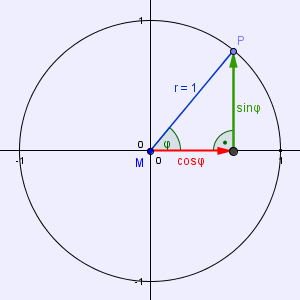
Abb. 6 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
So können nun im 1. Quadranten die Werte von Sinus und Cosinus einfach abgemessen und abgelesen werden.
Um den Tangens ähnlich einfach bestimmen zu können, suchen wir nun ein Dreieck dessen Ankathete zum Mittelpunktswinkel φ gleich 1 ist.
Somit erhalten wir dann ähnlich wie bei Sinus und Cosinus:
Gegenkathete Gegenkathete
tan(φ) = - - - - - - - - - - - - = - - - - - - - - - - - - = Gegenkathete
Ankathete 1
Dieses Dreieck finden wir, indem am Punkt (1/0) eine Tangente an den Einheitskreis angelegt wird und die Strecke vom Mittelpunkt M zum Punkt P bis zum Schnittpunkt mit der Tangente verlängert wird.
So entsteht nun folgendes Bild (siehe Abb. 7):
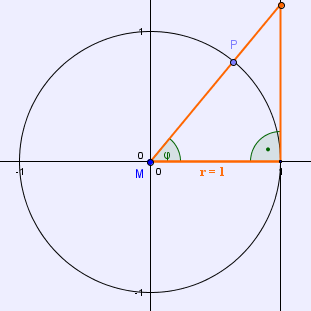
Abb. 7 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
Der Tangens (tan(φ)) entspricht also der Gegenkathete dieses Dreiecks, wodurch nun wieder der Wert einfach abgemessen und abgelesen werden kann.
Zusammengefasst erhält man jetzt eine Skizze (Abb. 8) für alle Winkelfunktionen im 1. Quadranten des Einheitskreises:

Abb. 8 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
|
|
3.3 Zusammenfassung und Folgerungen für alle vier Quadranten
|

 

|
Der SINUS wird auf der senkrechten Kathete abgelesen, entspricht also der Y-KOORDINATE von P.
Der COSINUS wird auf der waagrechten Kathete abgelesen, entspricht also der X-KOORDINATE von P.
Der TANGENS wird auf Tangente abgelesen, die im Punkt (1/0) den Einheitskreis berührt, entspricht also der Y-KOORDINATE des Schnittpunktes der Tangente mit der verlängerten Strecke MP.
Ist die entsprechende Koordinate also negativ, ist auch der Wert der jeweiligen Winkelfunktion negativ.
Hier folgen zwei Abbildungen (Abb. 9, Abb. 10) die diese Merksätze verdeutlichen sollen.
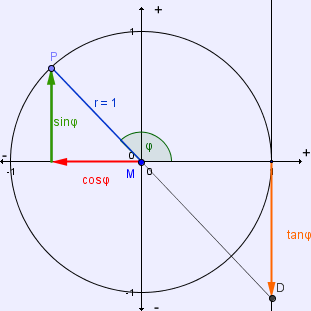
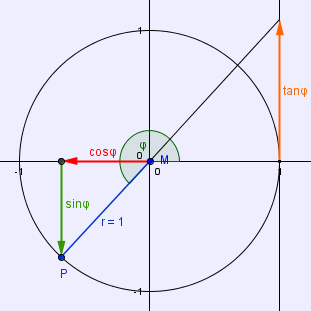
Abb. 9 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/) Abb. 10 (Langmann, https://www.mathe-online.at/lernpfade/einheitskreis/)
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



