| | |
| | | |
| |
| | |
| | | |
| |
| | |
Die Fourierreihe ist ein nützliches mathematisches Werkzeug, das in der Elektro- und Nachrichtentechnik, in der Akustik,
der Optik und der Quantentheorie sowie in zahlreichen anderen physikalischen Gebieten eingesetzt wird. Bevor wir sie besprechen,
müssen wir einige Vorarbeiten leisten.
| | | |
| |
| | |
Die trigonometrischen Basisfunktionen zur Periode 2π
Vom Standpunkt der periodischen Funktionen Sinus und Cosinus betrachtet, ist die "natürlichste" Zahl nicht
1, sondern
2π, denn es gilt
| | | |

Periodizität
| |
| | |
für alle reellen Zahlen x,
und 2π ist die kleinste Zahl mit dieser Eigenschaft.
Wir nennen sie die Periode (oder Periodenlänge) der Sinus- und der Cosinusfunktion.
(Die Beziehungen (1) und (2) gelten sogar für
alle komplexen Zahlen x, aber das
werden wir hier nicht benötigen).
Wie aus den Graphen der beiden Funktionen
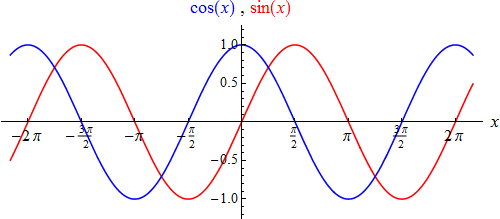
ersichtlich ist, hängen sie auch untereinander durch eine einfache Beziehung zusammen:
In diesem Sinn sind sie nur "verschobene" Versionen voneinander. Zu ihren zahlreichen Anwendungen zählt die
Beschreibung von Schwingungsvorgängen. Hat die Variable
x die Bedeutung der Zeit (oder einer
Größe, die proportional zur Zeit ist), und wird sie in der obigen Skizze gleichmäßig von links
nach rechts durchlaufen, so beschreibt das Verhalten der Funktionswerte ein regelmäßiges ("harmonisches")
Auf und Ab, zwischen den Werten –1
und 1.
Doppelt so schnelle Vorgänge
werden durch die Funktionen
sin(2x)
und
cos(2x)
beschrieben, dreimal so schnelle Vorgänge
durch die Funktionen
sin(3x)
und
cos(3x),
usw.
Für das Folgende werden wir auch eine Funktion benötigen, die überhaupt keine Schwingung beschreibt,
sondern konstant ist. Dafür wählen wir die Funktion, die konstant
1 ist.
All diese Funktionen gemeinsam wollen wir die trigonometrischen Basisfunktionen zur Periode
2π nennen. Fassen wir sie zusammen:
|
|
(4a) |
|
cos(nx)
für n = 1, 2, 3, ...
|
|
|
(4b) |
|
sin(nx)
für n = 1, 2, 3, ...
|
|
|
(4c) |
Die konstante Funktion 1 gehört in gewisser Weise zur Gruppe der
Cosinusfunktionen, da wir sie als Spezialfall von
cos(nx)
mit n = 0 ansehen können. (Erinnern Sie sich bzw. lesen Sie am
obigen Graphen der Cosinusfunktion ab, dass
cos(0) = 1 gilt).
Für die Funktionen
sin(nx)
hingegen würden wir mit n = 0
lediglich die konstante Funktion 0 bekommen.
Die Graphen der ersten vier Funktionen der Gruppe (4a) – (4b) sehen so aus:
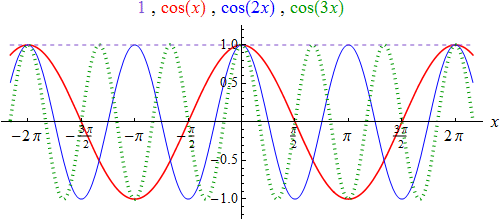
Die Graphen der ersten drei Funktionen der Gruppe (4c) sehen so aus:
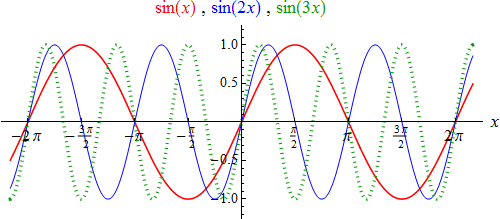
Die Graphen der Funktionen
sin(nx)
und
cos(nx)
für n > 1 werden aus jenen von
sin(x)
und
cos(x)
durch entsprechende "Stauchungen" in x-Richtung erhalten.
Denkt man sich x als Zeit, so entsprechen
| | | |

komplexe Zahlen
| |
| | |
- sin(x)
und
cos(x)
der Grundschwingung eines Systems (mit Periode 2π),
- sin(2x)
und
cos(2x)
der ersten Oberschwingung (sie besitzen die Periode
π
und daher auch die Periode 2π),
- sin(3x)
und
cos(3x)
der zweiten Oberschwingung (sie besitzen die Periode
2π/3
und daher auch die Periode 2π), usw.
Wir haben hier die Einzahl – "Grundschwingung" und "Oberschwingung" – verwendet, da sich die den Sinus- und den Cosinusfunktionen entsprechenden
Schwingungen voneinander wegen (3) nur durch eine zeitliche Verschiebung unterscheiden, also physikalisch nicht wirklich unterschiedlich sind.
Durch die Entlehnung eines Begriffs aus der Akustik können wir allgemein
n als Frequenz ansehen:
- n = 1 ist dann die Grundfrequenz, die
der Grundschwingung (oder dem Grundton) entspricht,
- und ihre ganzzahligen Vielfachen
n = 2, 3, ...
sind die höheren Freqzenzen, die den Oberschwingungen (oder Obertönen) entsprechen.
Wenn es Sie stört, dass x dimensionslos ist und daher genau genommen
keine Zeit darstellen kann, so stellen Sie sich einfach vor, dass x
die Zeit in Sekunden angibt.
Die höheren Basisfunktionen besitzen zwar auch kleinere Periodenlängen als
sin(x)
und
cos(x)
– und die konstante Funktion 1 besitzt jede Zahl als Periodenlänge –, aber wir
wollen in den nun folgenden Überlegungen immer 2π
als die Basisperiode, auf die wir uns beziehen, ansehen.
| | | |
Betrachtungen zur
| |
| | |
Orthogonalität
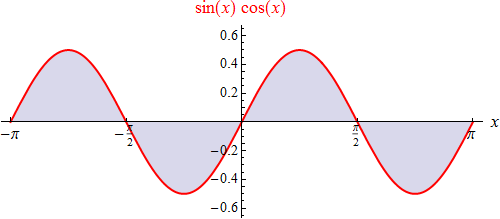
Die trigonometrischen Basisfunktionen besitzen eine bemerkenswerte Eigenschaft, die mit dem Integrieren zusammenhängt.
Sehen wir uns einmal den Graphen des Produkts
sin(x)
cos(x) an:
| | | |

integrieren
| |
| | |
Über jedes Intervall hinweg betrachtet, dessen Länge mit der Periode 2π
übereinstimmt, liegt gleich viel Flächeninhalt oberhalb wie unterhalb der
x-Achse. Da das bestimmte Integral den
orientierten Flächeninhalt zwischen Graph und x-Achse misst
(also Flächenstücke unterhalb der x-Achse
negativ wertet), gilt offenbar
| |
|
|
c + 2π |
|
|
|
|
∫ |
|
sin(x)
cos(x) dx |
= 0
, |
| |
|
|
c |
|
|
(6) |
und zwar unabhängig davon, welcher Wert für die untere Grenze
c angenommen wird. Üblicherweise wird in derartigen Ausdrücken
das Intervall symmetrisch zum Nullpunkt gewählt, also
c = –π gesetzt, womit (6)
die Form
| |
|
|
π |
|
|
|
|
∫ |
|
sin(x)
cos(x) dx |
= 0
|
| |
|
|
–π |
|
|
(6b) |
annimmt. Das Gleiche können wir mit zwei beliebigen unserer Basisfunktionen machen, solange sie verschieden
sind: So sieht etwa der Graph des Produkts
sin(2x)
cos(3x) so aus:
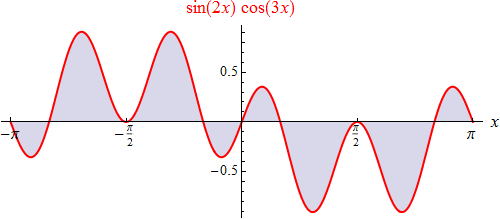
Wieder scheint das bestimmte Integral über eine vollständige Basisperiode zu verschwinden:
| |
|
|
π |
|
|
|
|
∫ |
|
sin(2x)
cos(3x) dx |
= 0
. |
| |
|
|
–π |
|
|
(7) |
Die exakte Berechnung zeigt, dass (6), (6b) und (7)
tatsächlich gelten.
| | | |

Intervalle

bestimmtes Integral

orientierter Flächeninhalt
| |
| | |
Aufgabe: Führen Sie den Beweis von (6b) selbst durch! Hier nur ein Tipp: Eine Stammfunktion von
sin(x)
cos(x)
ist
sin2(x)/2.
Auch das Integral über das Produkt zweier verschiedener Sinus-Basisfunktionen oder
zweier Cosinus-Basisfunktionen ist gleich 0, und das Gleiche gilt für die
Integrale über die Sinus-Basisfunktionen und Cosinus-Basisfunktionen selbst (die mit der konstanten Funktion
1 multipliziert ja wieder sich selbst ergeben). Ganz allgemein gilt der
folgende
Satz: Für beliebige
m = 1, 2, 3, ... gelten die Beziehungen
| |
|
π |
|
|
π |
|
| |
|
∫ |
|
sin(mx) dx |
= |
|
∫ |
|
cos(mx) dx |
= 0
. |
| |
|
–π |
|
|
–π |
|
|
(8) |
Für beliebige
m = 1, 2, 3, ... und
n = 1, 2, 3, ... mit
m ≠ n gelten die
Beziehungen
| |
|
π |
|
|
|
π |
|
| |
|
∫ |
|
sin(mx)
sin(nx) dx |
=
|
|
|
∫ |
|
cos(mx)
cos(nx) dx |
= 0
, |
| |
|
–π |
|
|
|
–π |
|
|
(9a) |
und für beliebige
m = 1, 2, 3, ... und
n = 1, 2, 3, ... gilt
| |
|
π |
|
| |
|
∫ |
|
sin(mx)
cos(nx) dx |
= 0
. |
| |
|
–π |
|
|
(9b) |
Anstelle des Integrationsintervalls [–π, π]
kann auch jedes Intervall der Form [c, c + 2π]
genommen werden, also beispielsweise
[0, 2π]. |
| | | |

Stammfunktion
| |
| | |
Der Beweis dieses Satzes kann am einfachsten mit Hilfe einer weiteren bemerkenswerten Eigenschaft der Sinus- und der Cosinusfunktion
geführt werden. Die Eulersche Formel gestattet es, diese auf die (leichter zu integrierende) Exponentialfunktion
zurückzuführen:
Eulersche Formel: Für beliebige (reelle oder komplexe)
x gilt
|
eix =
cos(x) + i
sin(x)
.
|
|
|
(10) |
Damit können die Sinus- und die Cosinusfunktion in der Form
| sin(x)
= |
1
2i |
|
( |
eix
– e–ix |
) |
und cos(x)
= |
1
2 |
( |
eix +
e–ix |
) |
|
|
(11) |
durch die (komplexe) Exponentialfunktion ausgedrückt werden.
|
| | | |

Eulersche Formel
| |
| | |
Der Beweis von (8) – (9b) ist dann eine sehr einfache Übung in Integration der Exponentialfunktion
(siehe den nebenstehenden Button).
Die Formeln (8) – (9b) können auf eine Weise, die Sie jetzt vielleicht überraschen wird,
gedeutet werden: Sie besagen, dass die trigonometrischen Basisfunktionen in einem gewissen Sinn "aufeinander normal stehen".
Doch halt – wie können Funktionen aufeinander normal stehen? Ist die Eigenschaft des Aufeinander-normal-Stehens nicht
den Richtungen in Ebene und Raum und Objekten wie Vektoren in Ebene und Raum vorbehalten? Ja und nein!
Im geometrischen Sinn von "bilden zueinander einen Winkel von 90°" ist sie das tatsächlich, aber wir haben hier eine
Verallgemeinerung im Sinn. Dazu rufen wir uns in Erinnerung, dass das Skalarprodukt von Vektoren
durch Formeln wie
|
u · v = u1v1 + u2v2
bzw.
u · v = u1v1 + u2v2 + u3v3
|
|
|
(12) |
definiert ist. (Im Unterschied zum zweiten Vektorkapitel schreiben wir hier einen Punkt, um das Skalarprodukt zu kennzeichnen).
Zwei Vektoren
u
und
v
stehen aufeinander normal, wenn ihr Skalaprodukt gleich
0 ist, d.h. wenn
u · v = 0
gilt.
Für das durch (12) definierte Skalarprodukt gelten nun bestimmte Rechenregeln, die darauf hinauslaufen, dass
wir Klammern mit Skalarprodukten genauso ausmultiplizieren können wie mit gewöhnlichen Produkten von Zahlen, dass
stets
u · v =
v · u gilt, und dass
die Beziehung
u · u = 0
nur für u = 0 gilt.
Mathematiker und Mathematikerinnen haben nun den Hang, derart schöne Strukturen auf andere Menge zu übertragen. Wenn wir insbesondere
zwei Funktionen
f und
g, die auf dem Intervall
[–π, π] definiert sind, die Zahl
| |
|
|
π |
|
| f · g
= |
|
|
∫ |
|
f (x)
g(x) dx |
|
| |
|
|
–π |
|
|
(13) |
zuordnen (Achtung: mit
f · g
wird hier nicht die Produktfunktion
x ® f (x) g(x)
bezeichnet, sondern deren Integral!),
so ergeben sich für diese Operation genau die gleichen Gesetze für das Rechnen mit Klammern wie für das Skalarprodukt
von Vektoren, und wie für dieses gilt stets
f · g =
g · f.
Bei der letzten Regel müssen wir etwas aufpassen: Da der Ausdruck
f · f
das Integral über ein Quadrat einer Funktion (das ja immer
≥ 0
ist) darstellt, gilt die Beziehung
f · f =
0 nur für Funktionen, die entweder überall gleich
0 sind oder nur an so wenigen Stellen
≠ 0, dass das Integral nichts davon bemerkt.
Diese kleine Komplikation ignorieren wir, und wir bezeichnen die Operation (13) als
Skalarprodukt für Funktionen, die auf dem Intervall
[–π, π] definiert sind.
Auch in formaler Hinsicht ähnelt (13) den Formeln (12):
Statt der Summe steht ein Integral, und anstelle der Komponenten
u1,
u2,... stehen nun
die Funktionswerte f (x).
Die Variable x entspricht dem Index, der die
Vektorkomponenten durchnummeriert.
Auf der Basis des Skalarprodukts (13) können wir nun zwei auf dem Intervall [–π, π] definierte Funktionen
f und g
als zueinander orthogonal bezeichnen, wenn
f · g =
0 ist.
Mit diesem Begriff von Orthogonalität besagen die Formeln (8) – (9b) nichts
anderes, als dass je zwei (verschiedene) trigonometrische Basisfunktionen zueinander orthogonal
sind.
| | | |

Skalarprodukt
| |
| | |
Normierung
Bevor wir zum eigentlichen Thema dieses Kapitels kommen – den Fourierreihen – müssen wir noch eine
Frage stellen: Wenn die Formeln (8) – (9b) besagen, dass
je zwei (verschiedene) trigonometrische Basisfunktionen bezüglich des
Skalarprodukts (13) zueinander orthogonal sind, was ist dann eigentlich das Skalarprodukt einer
solchen Funktion mit sich selbst? In Analogie zur Geometrie der Vektoren können wir ein Skalarprodukt der Form
f · f
als Quadrat der "Länge" (oder besser als Normquadrat) einer solchen Funktion auffassen. Die dafür
nötigen Integrale können mit Hilfe der Eulerschen Formel (10) leicht berechnet werden
(siehe den nebenstehenden Button). Die Ergebnisse sind:
Satz: Für beliebige
n = 1, 2, 3, ... gilt
| |
|
π |
|
|
π |
|
| |
|
∫ |
|
sin2(mx) dx |
= |
|
∫ |
|
cos2(mx) dx |
= π
. |
| |
|
–π |
|
|
–π |
|
|
(14) |
Das Integral der konstanten Funktion 1
über das Intervall [–π, π]
ist natürlich gleich 2π.
|
| | | |
| |
| | |
Im Sinne des Skalarprodukts (13) hat die konstante Funktion 1
die Norm (2π)1/2,
alle anderen trigonometrischen Basisfunktionen haben die Norm π1/2.
Damit können wir die trigonometrischen Basisunktionen als geometrische Objekte deuten:
Sie sind Elemente eines Raumes mit unendlicher Dimension, sind zueinander orthogonal und haben die soeben berechneten
Normquadrate (also "Längenquadrate"). Im Folgenden spielen Sie eine ähnliche Rolle wie die drei Vektoren der Standardbasis
des dreidimenaionalen Raumes R3,
die ebenfalls aufeinander normal stehen, und in die sich jeder räumliche Vektor entwickeln lässt.
|
| | |

Standardbasis
| |
| | |
| Fourierreihe mit Periode 2π |
| | | |
Zum Seitenanfang | |
| | |
| | | |
| |
| | |
Idee einer Reihenentwicklung
Eine spezielle Form von Reihenentwicklung kennen Sie wahrscheinlich bereits: die Potenzreihenentwickung.
Sie besteht darin, eine gegebene Funktion als "unendliche Linearkombination" von Funktionen der Form
xn (mit
n = 0, 1, 2, 3, ...), also – wenn Sie so wollen –
als "unendliches Polynom" (eben als Potenzreihe) darzustellen. Eine der bekanntesten und wichtigsten Potenzreihenentwicklungen
ist die der Exponentialfunktion:
|
ex = 1 + x + x2/2 +
x3/6 + x4/24 + ...
.
|
|
|
(15) |
Die Zahlen
1,
1,
1/2,
1/6,...
treten hier als Koeffizienten der Funktionen
1,
x,
x2,
x3,... auf, in die eine Funktion "entwickelt wird".
So eine Entwicklung lässt sich nicht mit jeder Funktion durchführen, aber immerhin mit den
interessantesten. Eine mögliche Anwendung besteht darin, eine Funktion durch ein
Polynom zu approximieren, indem nur endliche viele Reihenglieder angegeben werden. So gilt für kleine
x
|
ex ≈ 1 + x + x2/2 +
x3/6
.
|
|
|
(16) |
Die Fourierreihe ist eine ähnliche Konstruktion, wobei an die Stelle der Funktionen
1,
x,
x2,
x3,...
die trigonometrischen Basisfunktionen treten.
| | | |

Potenzreihen

Exponentialfunktion
zur Basis
e
| |
| | |
Endlich: die Fourierreihe
Nach so vielen Vorarbeiten kommen wir nun ohne weitere Umschweife zur Fourierreihe mit Periode
2π.
Sie beruht auf einer weiteren Eigenschaft der trigonometrischen Basisfunktionen
(4a) – (4c), die wir allerdings nicht beweisen: Sie sind
vollständig in den Sinn, dass sich eine große Klasse von Funktionen durch sie
beliebig genau approximieren lässt. Wir formulieren diesen Sachverhalt als
Satz: Jede
auf dem Intervall [–π, π]
definierte stückweise stetige und beschränkte
Funktion f
kann als Fourierreihe in der Form
| f (x)
= |
a0
2 |
+
a1 cos(x) +
a2 cos(2x) +
a3 cos(3x) + ... +
b1 sin(x) +
b2 sin(2x) +
b3 sin(3x) + ...
|
|
|
(17a) |
oder, in Summenschreibweise,
| |
|
|
∞ |
|
| f (x)
= |
a0
2 |
+ |
∑ |
|
( an
cos(nx)
+ bn
sin(nx) ) |
|
| |
|
|
n = 1 |
|
|
(17b) |
dargestellt werden. An allen Stellen x, an denen
f stetig ist, konvergiert die Reihe gegen
den Funktionswert f (x).
An den Unstetigkeitsstellen konvergiert die Reihe gegen den Mittelwert aus
linksseitigem und rechtsseitigem Grenzwert.
(Für diese Stellen ist das Gleichheitszeichen in (17a) und (17b) also
möglicherweise nicht gültig).
Die Entwicklung einer Funktion in eine Fourierreihe kann als Zerlegung der Funktion in die durch die trigonometrischen
Basisfunktionen dargestellten Schwingungen verstanden werden und heißt Fourieranalyse.
|
| | | |

stückweise stetig

beschränkt

links- und rechtsseitiger Grenzwert
| |
| | |
Wir machen nun einige Bemerkungen dazu:
- Der Koeffizient der konstanten Funktion 1
wurde in (17a) und (17b)
als a0/2 und nicht als
a0 geschrieben. Der Grund dafür liegt darin, dass
die konstante Funktion 1
eine andere Norm besitzt als die anderen trigonometrischen Basisfunktionen. Diese Konvention wird einige der folgenden Beziehungen
vereinfachen.
Der Koeffizient von
cos(nx)
ist an, jener von
sin(nx)
ist bn.
- (17a) und (17b) wurden für Funktionen definiert,
die auf dem Intervall [–π, π]
definiert sind. Stimmen die Funktionswerte bei
–π und bei
π überein, so kann eine solche Funktion
zu einer für alle reellen Zahlen definierten periodischen Funktion mit Periode
2π fortgesetzt werden. Umgekeht kann jede periodische
Funktion auf unser Basisintervall [–π, π]
eingeschränkt werden. Ob wir also bei der Fourierreihe von periodischen Funktionen sprechen oder von Funktionen, die auf dem
Basisintervall definiert sind, ist im Grunde gleichgültig.
- Tatsächlich kann eine noch größere Klasse von Funktionen in eine Fourierreihe entwickelt werden, als bei der
Formulierung des Satzes angegeben ist. In der Praxis werden aber meist stückweise stetige Funktionen betrachtet.
Differenzierbarkeit ist also keine notwendige Voraussetzung (im Unterschied zur Potenzreihenentwicklung)!
- Wird eine Fourierreihe nach endlich vielen Gliedern abgebrochen, so ergibt sich eine Approximation der
betreffenden Funktion durch endlich viele trigonometrischen Basisfunktionen. Eine nach endlich vielen Gliedern "abgebrochene" Fourierreihe
wird auch trigonometrisches Polynom genannt. Ein Maß dafür, wie gut eine Funktion
f durch ein solches trigonometrisches Polynom
approximiert wird, ist das Integral
| |
|
|
π |
|
|
|
|
∫ |
|
( f (x)
– trigonometrisches Polynom (x) )2
dx
. |
|
| |
|
|
–π |
|
|
(18) |
In der Sprechweise, die sich auf das Skalarprodukt (13)
bezieht, entspricht es dem Quadrat der Norm (d.h. dem Quadrat der "Länge") der Differenz
f – trigonometrisches Polynom.
Werden immer mehr Glieder der Fourierreihe hinzugefügt, so strebt es gegen 0.
Diese Eigenschaft beschreibt die Art der Konvergenz, die
hinter dem Konzept der Fourierreihe steckt. Sie wird Konvergenz im quadratischen Mittel genannt. Ein anderer Name dafür ist
Konvergenz in der L2-Norm (nach einem Fachausdruck, dessen genaue Erläuterung uns hier zu weit führen würde).
| | | |
| |
| | |
Die Entwicklungskoeffizienten
Lassen wir die Details beiseite, so sagt der obige Satz aus, dass eine gegebene Funktion mit Periode
2π in einer Fourierreihe entwickelt werden kann.
Sei also f eine solche Funktion.
Dann wüssten wir gern die Werte der Entwicklungskoeffizienten (Fourierkoeffizienten)
- a0,
- an (für
n = 1, 2, 3, ...)
- und
bn (für
n = 1, 2, 3, ...).
Nach unserer umfangreichen Vorarbeit ist es nun
ganz leicht, sie zu berechnen. Wir nehmen an, die Funktion f
sei bereits als Fourierreihe (17a) bzw. (17b) dargestellt.
- Berechnung von a0:
Wir bilden das bestimmte Integral der rechten Seite von (17a) bzw. (17b) über das
Intervall [–π, π].
Da aufgrund von (8) die Integrale über alle auftretenden Sinus- und Cosinusfuntionen verschwinden,
trägt nur der erste (konstante) Term bei. Der Wert des Integrals ist gleich
π a0.
Diesen setzen wir gleich dem Integral der linken Seite,
lösen nach a0 auf und erhalten
- Berechnung von an für
n = 1, 2, 3, ...:
Wir multiplizieren die rechte Seite von (17a) bzw. (17b) mit einer der
trigonometrischen Cosinus-Basisfunktionen, beispielsweise
cos(3x),
und bilden danach das bestimmte Integral über das
Intervall [–π, π].
Da aufgrund von (8) – (9b) die Integrale über alle Produkte von verschiedenen
Basisfunktionen verschwinden, trägt nur ein einziger Term bei, und zwar jener, in dem
cos(3x)
mit sich selbst multipliziert wird. Mit (14) ergibt sich der Wert des Integrals zu
π a3. Diesen setzen wird gleich dem Integral
über das Produkt der linken Seite mit
cos(3x)
und lösen nach a3 auf.
Der gleiche Methode kann mit jedem Cosinusterm durchgeführt werden – der Vorgang ist stets der gleiche –,
woraus sich ganz allgemein ergibt:
| |
|
|
π |
|
| an
= |
1
π |
|
∫ |
|
f (x)
cos(nx) dx |
|
| |
|
|
–π |
|
|
(20) |
|
- Berechnung von bn für
n = 1, 2, 3, ...:
Wir multiplizieren die rechte Seite von (17a) bzw. (17b) mit einer der
trigonometrischen Sinus-Basisfunktionen, beispielsweise
sin(3x),
und bilden danach das bestimmte Integral über das
Intervall [–π, π].
Da aufgrund von (8) – (9b) die Integrale über alle Produkte von verschiedenen
Basisfunktionen verschwinden, trägt nur ein einziger Term bei, und zwar jener, in dem
sin(3x)
mit sich selbst multipliziert wird. Mit (14) ergibt sich der Wert des Integrals zu
π b3. Diesen setzen wird gleich dem Integral
über das Produkt der linken Seite mit
sin(3x)
und lösen nach b3 auf.
Der gleiche Methode kann mit jedem Sinusterm durchgeführt werden – der Vorgang ist stets der gleiche –,
woraus sich ganz allgemein ergibt:
| |
|
|
π |
|
| bn
= |
1
π |
|
∫ |
|
f (x)
sin(nx) dx |
|
| |
|
|
–π |
|
|
(21) |
|
| | | |
| |
| | |
Mit (19), (20) und (21) haben wir das Problem, die Entwicklungskoeffizienten zu einer
gegebenen Funktion zu finden, gelöst. Im Unterschied zur Potenzreihenentwicklung einer gegebenen
Funktion (der Taylorreihe, deren Entwicklungskoeffizienten
durch Differenzieren gefunden werden) müssen wir im Fall der Fourierreihe Integrale berechnen, um sie zu bestimmen.
Einige Bemerkungen dazu:
- Die Formeln (19), (20) und (21) machen klar, dass die Fourierreihe gewissermaßen "blind"
für das Verhalten von f in einzelnen Punkten ist.
Wird beispielsweise ein Funktion dadurch abgeändert, dass sie an einem einzigen Punkt neu definiert wird, so bleibt ihre
Fourierreihe gleich.
- Anstelle des Integrationsintervalls [–π, π]
kann in den Integralen (19), (20) und (21)
auch jedes Intervall der Form [c, c + 2π]
genommen werden, also beispielsweise
[0, 2π].
- Die Formeln (19), (20) und (21) haben alle eine ähnliche Form. Das war der Grund
dafür, den Koeffizienten der konstanten Funktion 1
in (17a) bzw. (17b)
als a0/2 anzusetzen und nicht als
a0.
- (19) und (20) können zusammengefasst werden, indem in
(20) auch n = 0
zugelassen wird. (Erinnern Sie sich, dass
cos(0) = 1 gilt).
Damit sind wir ausgerüstet, einen gegebene Funktion mit Periode
2π in eine Fourierreihe zu entwickeln. Bevor wir uns ein
paar Beispiele ansehen, erwähnen wir noch einen Sachverhalt, der helfen kann, Berechnungen abzukürzen, und geben
Tipps hinsichtlich des Umgangs mit den auftretenden Integralen.
| | | |

Taylorreihe
| |
| | |
Symmetrische und antisymmetrische Funktionen
Für manche Funktionen kann die "Hälfte" der Entwicklungskoeffizienten auch ohne Integration bestimmt werden.
Wie im zweiten Funktionenkapitel definiert, nennen wir eine Funktion
f symmetrisch (oder gerade), wenn
und antisymmetrisch (oder ungerade), wenn
für alle x.
Der Graph einer symmetrischen Funktion geht durch eine Spiegelung an der
y-Achse in sich selbst über.
Der Graph einer antisymmetrischen Funktion geht durch eine Punktspiegelung am
Ursprung (d.h. durch eine Drehung im 180°) in sich selbst über. Weiters gilt
- Das Produkt zweier symmetrischer Funktionen ist symmetrisch.
Beweis:
f (–x)
g(–x) = f (x) g(x).
- Das Produkt zweier antisymmetrischer Funktionen ist symmetrisch.
Beweis:
f (–x)
g(–x) =
(–f (x)) (–g(x)) =
f (x) g(x).
- Das Produkt einer symmetrischen und einer antisymmetrischen Funktionen ist antisymmetrisch.
Beweis:
f (–x)
g(–x) =
f (x) (–g(x)) =
– f (x) g(x).
- Jede konstante Funktion und jede Funktion der Form
cos(nx)
ist symmetrisch.
- Jede Funktion der Form sin(nx)
ist antisymmetrisch.
Der springende Punkt ist nun: Das Integral einer antisymmetrischen Funktion über ein symmetrisches Integrationsintervall
wie [–π, π] ist gleich
0, denn zwischen ihrem Graphen und
der x-Achse liegt gleich viel Flächeninhalt
oberhalb wie unterhalb derselben. Daraus ergeben sich folgende Regeln für die Entwicklungskoeffizienten
(19), (20) und (21):
- Ist f eine symmetrische Funktion, so ist
bn = 0 für
n = 1, 2, 3, ...
Beweis: Alle Produkte
f (x)
sin(nx) sind antisymmetrisch. Daher ist das Integral
in (21) gleich 0.
- Ist f eine antisymmetrische Funktion, so ist
a0 = 0 und
an = 0 für
n = 1, 2, 3, ...
Beweis: f selbst sowie alle Produkte
f (x)
cos(nx) sind antisymmetrisch. Daher sind die Integrale
in (19) und (20) gleich 0.
Diese Regeln zu beachten, kann beim Berechnen von Funktionen viel Arbeit sparen!
Sie können sie sich auch so merken:
- Die Funktionen
1 und
cos(nx)
sind symmetrisch. Sie spannen den Raum der symmetrischen Funktionen auf.
- Die Funktionen
sin(nx)
sind antisymmetrisch. Sie spannen den Raum der antisymmetrischen Funktionen auf.
|
Symmetrische und antisymmetrische Funktionen sind bezüglich des Skalarprodukts (13)
zueinander orthogonal.
Das erste Integral in (8) und die Beziehung
(9b) drücken genau genommen lediglich diese Orthogonalität aus.
Daher hat die Fourierreihe einer symmetrischen Funktion keinen antisymmetrischen Anteil, und
die Fourierreihe einer antisymmetrischen Funktion hat keinen symmetrischen Anteil.
| | | |

symmetrisch (gerade) und antisymmetrisch (ungerade)
| |
| | |
Tipps zur Berechnung von Integralen
Wie bei der Berechnung der hier auftretenden Integrale am besten vorgegangen wird, hängt natürlich
von der konkreten Funktion f ab, die in eine
Fourierreihe entwickelt werden soll.
Die Schwierigkeit besteht darin, Integrale wie (20) und (21)
für alle n zu berechnen – also genau genommen
unendlich viele Integrale. In der Praxis werden oft Funktionen betrachtet, die
stückweise in Teilintervallen wie
[–π, 0] und
[0, π] durch einfache Terme definiert ist.
Wir wollen hier nicht auf die verschiedenen Berechnungsmethoden eingehen, sondern geben nur zwei Tipps:
- Integrale mit Winkelfunktionen können mit Hile der Eulerschen Formeln (10) und (11)
in Integrale über Exponentialfunktionen verwandelt werden, die leichter berechnet werden können.
- In jedem Fall können Sie ein Computeralgebra-System (CAS) oder das Online-Werkzeug
WolframAlpha
verwenden. In letzteres geben Sie beispielsweise zur Berechnung des Integrals
einfach
integrate x sin(n x) from x=0 to pi
ein.
Das Programm behandelt n als unbestimmte Zahl, weiß also
nicht, dass dieses Symbol in unserem Zusammenhang nur ganzzahlige Werte annehmen kann.
Wenn Sie die Ausgaben des Programms interpretieren und gegebenenfalls vereinfachen, beachten Sie,
dass für ganzzahlige n
stets
sin(πn) = 0
und
cos(πn) = (–1)n
gilt!
| | | |
| |
| | |
Für die Berechnung unbestimmter Integrale, d.h. von Stammfunktionen,
können Sie den
Wolfram Mathematica Online Integrator
verwenden. Wir werden im Folgenden nicht auf die Berechnung der auftretenden Integrale eingehen,
sondern lediglich die Ergebnisse angeben.
| | | |

Stammfunktion
(unbestimmtes
Integral)
| |
| | |
Beispiele
Jetzt ist es Zeit für ein paar Beispiele. Um anhand von Beispielen ein Gefühl für Fourierreihen zu bekommen, gibt es
zwei Möglichkeiten: Sie können vorgegebene Funktionen in Fourierreihen entwickeln, und Sie können mit
Fourierreihen spielen, in dem Sie trigonometrische Polynome vorgenen und ihre Graphen betrachten.
Für die zweite Möglichkeit steht das nebenstehende Applet
zur Verfügung. Stellen Sie die Schieberegler, die den ersten 11 Entwicklungskoeffizienten
entsprechen, nach Belieben ein und sehen Sie sich die Funktionsverläufe an, die daraus entstehen!
Die erste Möglichkeit ist etwas mühsamer, denn für sie müssen wir Integrale berechnen.
Beispiel 1:
Die Sägezahnfunktion ist in unserem Basisintervall definiert durch
und wird auf ganz R periodisch fortgesetzt.
Ihr Graph sieht so aus:
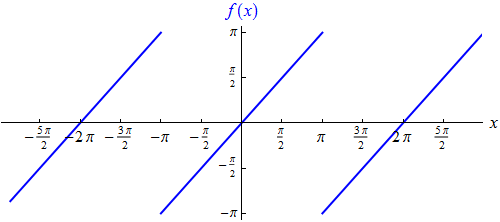
Sie ist bei allen ungeraden Vielfachen von π
unstetig. Welcher Wert ihr an diesen Stellen zugewiesen wird, ist für ihre Fourierreihe unerheblich.
Da sie eine antisymmetrische Funktion ist, gilt
a0 = 0 und
an = 0 für
n = 1, 2, 3, ....
Wir müssen also lediglich mit Hilfe von (21) die Entwicklungskoeffizienten
bn
berechnen. Mit (23) ergibt sich
| |
|
|
π |
|
| bn
= |
1
π |
|
∫ |
x
sin(nx) dx
= – |
2 (–1)n
n
|
. |
| |
|
|
–π |
|
|
(24) |
Damit ist die Fourierreihe der Sägezahnfunktion bestimmt.
Aus (24) entnehmen wir die Werte der ersten vier Koeffizienten zu
b1 = 2,
b2 = –1,
b3 = 2/3 und
b4 = –1/2.
Das aus den entsprechenden vier Termen bestehende trigonometrische Polynom
(wir wollen es g4 nennen)
approximiert die Sägezahnfunktion bereits in erkennbarer Weise, wenngleich noch nicht sehr genau:
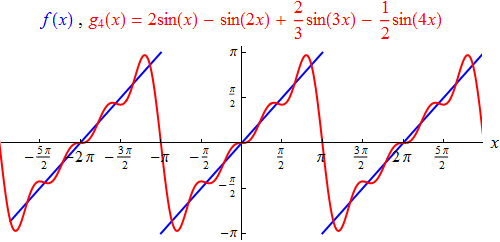
Das aus den ersten zehn Termen bestehende trigonometrische Polynom
g10
kommt der Sägezahnfunktion bereits näher:
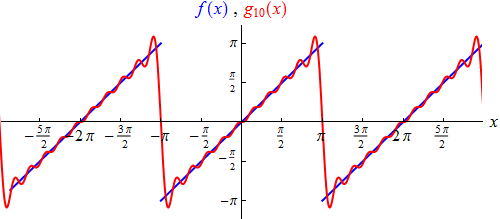
Nehmen wir immer mehr Reihenglieder dazu, so spielen die hinzukommenden höheren Frequenzen
mit den bereits vorhandenen auf wunderbare Weise zusammen, so dass die
Approximation mit den ersten 30 Termen der Reihe schon vielversprechend aussieht:
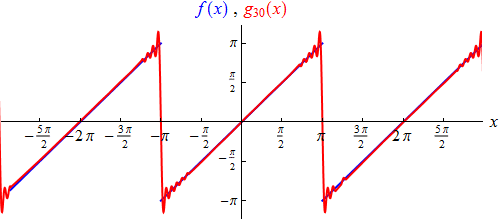
Lediglich in der Nähe der Unstetigkeitsstellen herrscht noch etwas Unruhe, die nicht
dem Verlauf der Sägezahnfunktion entspricht. Durch Hinzunahme weiterer Terme
können wir sie zwar zusammenschieben, aber nicht gänzlich loswerden, solange wir nur
endlich viele Reihenglieder betrachten. Das ist das so genannte Gibbssche Phänomen:
ein "Überschwingen" der abgebrochenen Fourierreihe in der Nähe jeder Unstetigkeitsstelle.
Erst wenn wir die vollständige Fourierreihe betrachten, so verschwindet es: Die
Reihe konvergiert dann überall außer an den Unstetigkeitsstellen gegen die
gegebene Funktion. An den Unstetigkeitsstellen konvergiert sie – wie bereits oben
erwähnt – gegen den Mittelwert aus linksseitigem und rechtsseitigem Grenzwert
der gegebenen Funktion, d.h. gegen den Wert 0.
Der Graph der von der Fourierreihe dargestellten Funktion (wir nennen sie
g∞)
sieht also so aus:
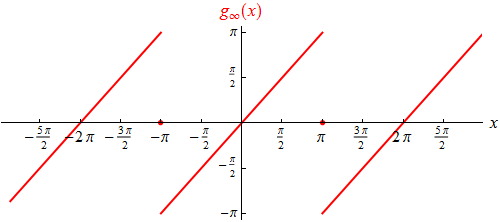
Er stimmt – außer an den Unstetigkeitsstellen, an denen wir f
gar nicht festgelegt haben – mit dem der Sägezahnfunktion überein.
Beispiel 2:
Der Dreiecksimpuls ist durch
|
f (x) = π – |x|
für –π ≤ x < π
|
|
|
(25) |
in unserem Basisintervall definiert und wird auf ganz R periodisch fortgesetzt.
Der Graph dieser Funktion sieht so aus:
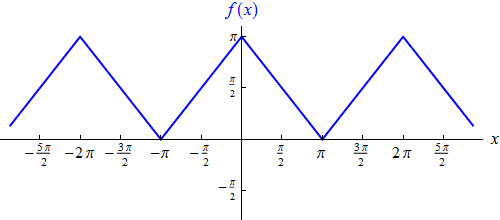
Es handelt sich diesmal um eine stetige Funktion. Sie ist symmetrisch, und daher gilt
bn = 0 für
n = 1, 2, 3, ....
Wir müssen also lediglich mit Hilfe von (19) und (20) die Entwicklungskoeffizienten
a0 und
an
für n = 1, 2, 3, ...
berechnen. Mit (25) ergibt sich
| |
|
|
π |
|
| a0
= |
1
π |
|
∫ |
(π – |x|)
dx
= π |
. |
| |
|
|
–π |
|
|
(26) |
Dieses Integral berechnen Sie entweder durch eine Zerlegung des Integrationsintervalls in zwei Teilintervalle,
was auf ein Integral von –π bis
0 und eines von
0 bis
π führt, oder Sie bemerken,
dass der Integrand in (26) symmetrisch ist, weshalb das Ergebnis zweimal dem
ersten Teilintegral ist, oder Sie lesen den Flächeninhalt unter dem Graphen ab,
ohne zu integrieren! Weiters finden wir
| |
|
|
π |
|
| an
= |
1
π |
|
∫ |
(π – |x|)
cos(nx) dx
= |
2 (1 – (–1)n)
π n2
|
|
| |
|
|
–π |
|
|
(27) |
für n = 1, 2, 3, ....
(Um dieses Integral – ohne den Vorfaktor 1/π
– mit WolframAlpha zu berechnen, geben
Sie
integrate (pi-abs(x)) cos(n x) from x=-pi to pi
ein und benutzen
cos(πn) = (–1)n
für ganzzahliges n). Daraus entnehmen wir
a1 = 4/π,
a2 = 0,
a3 = 4/(9π),
a4 = 0 und
a5 = 4/(25π).
Außer a0
verschwinden alle Koeffizienten mit geradem Index.
Das aus den ersten drei nichtverschwindenden Termen bestehende trigonometrische Polynom
g3
approximiert den Dreieckimpuls bereits recht gut:
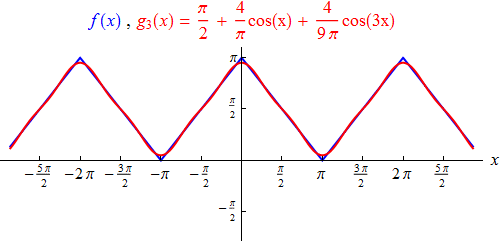
Beispiel 3:
Als nächstes Beispiel betrachten wir die (wieder periodisch auf ganz R
fortgesetzte) Treppenfunktion
Ihr Graph sieht so aus:
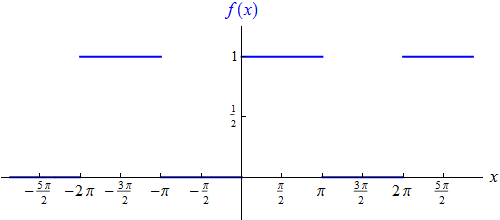
Diese Funktion ist weder symmetrisch noch antisymmetrisch, aber wenn Sie den Graphen genau anschauen, können Sie erkennen,
dass f (x) – 1/2
(eine Funktion, deren Graph im Vergleich zum obigen um 1/2 nach unten
verschoben ist) antisymmetrisch ist.
f (x) ist daher
1/2 plus eine antisymmetrische Funktion
(deren Fourierreihe demnach nur
sin(nx)-Anteile
besitzt).
Daher wissen wir von vornherein, dass
a0 = 1 gilt, und dass
alle anderen
an = 0 sind.
(Der umständliche Weg besteht natürlich darin, die entsprechenden Integrale zu berechnen).
Die verbleibenden Entwicklungskoeffizienten sind
| |
|
|
π |
|
| bn
= |
1
π |
|
∫ |
sin(nx) dx
= |
1 – (–1)n
π n
|
. |
| |
|
|
0 |
|
|
(29) |
Der Graph der nach den ersten zehn nichtverschwindenden Gliedern abgebrochene Fourierreihe sieht so aus:
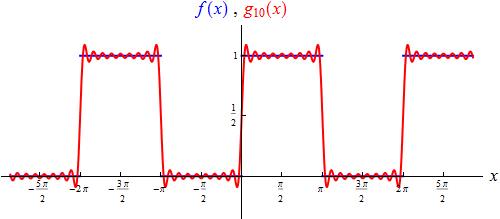
An ihm ist das Gibbssche Phänomen wieder recht schön zu erkennen. An den Unstetigkeitsstellen
von f konvergiert die Fourierreihe gegen den Wert
1/2.
Beispiel 4:
Unser letztes Beispiel ist eine Funktion, die nicht durch eine Termdarstellung, sondern von vornherein über ihre Fourierreihe definiert ist:
Es zeigt, dass Fourierreihen auch Funktionen darstellen können, die ganz unerwartete Eigenschaften besitzen:
| |
|
|
∞ |
|
| f (x)
= |
|
|
∑ |
|
2–k/2
sin(2kx)
=
sin(x)
+
2–1/2 sin(2x)
+
2–1 sin(4x)
+
2–3/2 sin(8x)
+ ...
|
. |
| |
|
|
k = 0 |
|
|
(30) |
| | | |
Applet
Fourierreihe
| |
| | |
Der Graph dieser Funktion (sofern man ihn überhaupt plotten kann) sieht so aus:
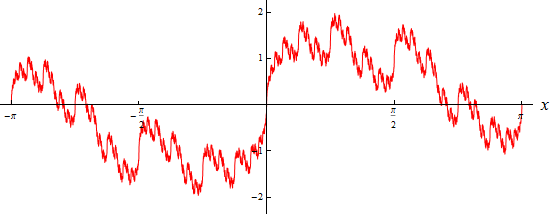
Sie ist in jedem Punkt stetig, aber in keinem Punkt differenzierbar!
Könnten sie sich näher an ihren Graphen heranzoomen, so würde er auch bei beliebiger Vergrößerung
ähnlich ausgefranst aussehen. Sie wurde im zweiten Kapitel zum Thema Differenzieren genauer diskutiert.
| | | |

stetig

nirgends
differenzierbar
Applet
Nirgends differenzierbare Funktionen
| |
| | |
Die spektrale Form der Fourierreihe
Wir sind nun in der Lage, eine gegebene Funktion mit Periode 2π
in eine Fourierreihe zu entwickeln. Stellen wir uns
x als Zeit vor, so bedeutet das,
einen zeitlich periodischen Vorgang in eine Grund- und unendlich viele Oberschwingungen zu zerlegen.
Mit einer solchen Zerlegung sind auch die Anteile der einzelnen Frequenzen
n bestimmt, die "in der Funktion stecken".
Da aber zu jeder Frequenz n
zwei Funktionen gehören, nämlich
cos(nx)
und
sin(nx),
und dementsprechend zwei Koeffizienten
an und
bn, muss der
entsprechende Frequenzanteil eine Kombination dieser beiden sein.
Er wird deutlicher sichtbar, wenn die Fourierreihe in einer leicht modifizierten Weise angeschrieben wird.
Dazu benutzen wir die Tatsache, dass jede Linearkombination der Form
auch mit Hilfe einer einzigen Sinus- oder Cosinusfunktion, einer Amplitude
A ≥ 0
und einer Phase φ geschrieben werden kann.
Wir entscheiden uns für die Form
Der Grund dafür, dass (31) stets auch in der Form (32) angeschrieben werden
kann, ist die Beziehung
|
cos(x – φ)
=
cos(x)
cos(φ) +
sin(x)
sin(φ)
|
, |
|
(33) |
die für beliebige x
und φ gilt. Damit können
(31) und (32) ineinander umgerechnet werden. Die Umrechnungsformeln
lauten
für die Amplitude und – wenn diese berechnet ist –
| | | |
| |
| | |
für die Phase φ
(die nur bis auf ein ganzzahliges Vielfaches von 2π bestimmt ist, was aber
keine Rolle spielt). Üblicherweise bildet man
b/a = tan(φ)
und berechnet φ mit Hilfe
des Arcus Tangens, aber je nach den Vorzeichen von
a und b
muss dann unter Umständen noch
π addiert werden, um
(34b) und (34c) zu erfüllen.
Formal haben wir hier mit diesen letzten beiden Formeln die gleichen Beziehungen vor uns, die wir benutzen,
um kartesische Koordinaten und ebene Polarkoordinaten ineinander umzurechnen.
Führen wir eine derartige Umformung für alle Linearkombinationen der Form
an cos(nx) +
bn sin(nx)
durch, so erhalten wir eine Form der Fourierreihe, in der die Frequenzanteile unmittelbar ersichtlich sind.
Die spektrale Form der Fourierreihe mit
Periode 2π
lautet
| f (x)
= |
A0
2 |
+
A1 cos(x – φ1) +
A2 cos(2x – φ2) +
A3 cos(3x – φ3) + ...
|
|
|
(35a) |
oder, in Summenschreibweise,
| |
|
|
∞ |
|
| f (x)
= |
A0
2 |
+ |
∑ |
|
An
cos(nx – φn)
|
. |
| |
|
|
n = 1 |
|
|
(35b) |
Die Konstanten
An ≥ 0
(für n = 1, 2, 3, ...)
bilden das
Amplitudenspektrum (auch Fourierspektrum oder Frequenzspektrum) von
f,
die Konstanten
φn bilden das
Phasenspektrum von f. Sie können aus der
Form (17a) bzw. (17b) durch die Beziehungen
sowie, für n = 1, 2, 3, ...,
und
ermittelt werden. In manchen Anwendungen ist nur das Amplitudenspektrum von Interesse.
Es ergibt sich – ohne, dass die Phasen
φn
berechnet werden müssten – mit (37) direkt aus der
früheren Form der Fourierreihe.
|
Das Amplitudenspektrum, d.h. die Gesamtheit der Konstanten
An
für n = 1, 2, 3, ...
ist die Antwort auf die Frage, wie viel von jeder Frequenz
n in
einer gegebenen Funktion f steckt.
Für das obige Beispiel 1 (23) sieht es so aus:
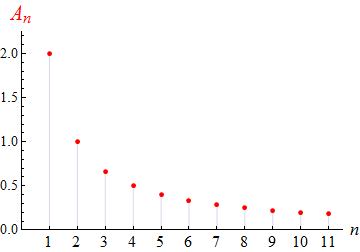
Für das obige Beispiel 2 (25) sieht es so aus:
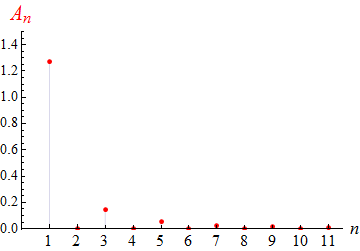
Für das obige Beispiel 3 (28) sieht es so aus:
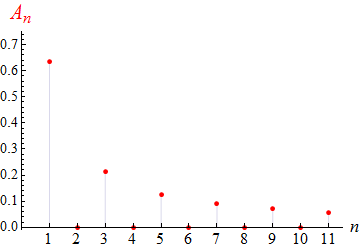
Ein interessanter Zug dieser Diagramme liegt in ihrem augenfälligsten Unterschied,
dem Abfallverhalten der An
für große n:
Im ersten und im dritten Beispiel fallen die An
wegen (24) und (29) wie 1/n ab,
im mittleren Beispiel wegen (27) wie 1/n2,
also viel schneller als in den beiden anderen Beispielen.
Sehen wir uns die Graphen der dargestellten Funktionen an, so erkennen wir einen anderen Unterschied: Die Funktionen
des ersten und dritten Beispiels sind unstetig, die im mittleren Beispiel ist stetig.
Das ist kein Zufall: Im Abfallverhalten des Amplitudenspektrums (das eine globale Eigenschaft
der Funktion
n ↦ An
ist) widerspiegeln sich häufig lokale Eigenschaften
wie Stetigkeit/Unstetigkeit oder der Grad an Differenzierbarkeit der dargestellten Funktion.
Wir gehen nicht auf die tieferen Gründe für Zusammenhänge dieser Art ein, sondern betrachten zuletzt das obige
Beispiel 4 (30), das eine nirgends differenzierbare Funktion darstellt. Ihr Amplitudenspektrum sieht so aus:
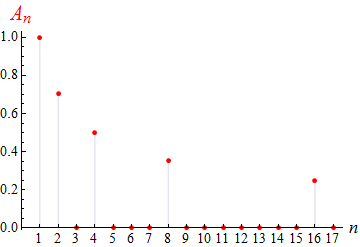
Hier sind nur jene An von
0 verschieden, für die
n eine Potenz von
2 ist
(also für n = 1, 2, 4, 8, 16, ...).
Die verbleibenden An
verhalten sich wie 1/n1/2
und fallen daher langsamer ab als in allen Beispielen zuvor. Ob nun in
f
ein "größerer" oder ein "kleinerer" Anteil hoher Frequenzen steckt als in den anderen Funktionen,
ist angesichts der vielen verschwindenden
An Ansichtssache, aber das Beispiel bewahrt
uns vor immerhin vor allzu vereinfachenden Schlüssen.
| | | |

Arcus Tangens

Polarkoordinaten
| |
| | |
Die komplexe Form der Fourierreihe
Die Eulerschen Formeln (10) und (11) erlauben es, die Funktionen
cos(nx)
und
sin(nx)
durch die komplexen Exponentialfunktionen
einx
und
e–inx
auszudrücken. Damit kann die Fourierreihe in einer für manche Zwecke geeigneteren – und vielleicht auch
ästetisch ansprechenderen – Form angeschrieben werden.
Die komplexe Form der Fourierreihe mit
Periode 2π
lautet
| |
|
|
∞ |
|
| f (x)
= |
|
|
∑ |
|
cn einx |
, |
| |
|
|
n = –∞ |
|
|
(39) |
wobei die Koeffizienten cn
für alle ganzzahligen n
direkt aus f
mittels der Formel
| |
|
|
π |
|
| cn
= |
1
2π |
|
∫ |
|
f (x)
e–inx dx |
|
| |
|
|
–π |
|
|
(40) |
bestimmt werden können. Die durch (39) dargestellte Funktion
f ist genau dann reellwertig, wenn
die Koeffizienten die Bedingung
erfüllen, wobei der Stern das komplex Konjugieren bezeichnet.
Der Zusammenhang zur Fourierreihe in der Form (17a) bzw. (17b) ist durch
gegeben, wobei (42b) und (42c)
für n = 1, 2, 3, ...
gelten.
|
Die komplexe Form der Fourierreihe wird in der Physik oft verwendet und ist unter anderem der Ausgangspunkt
für die Fouriertransformation, über die wir weiter unten noch
ein paar Worte sagen werden.
Nachbemerkung: Auch im Zusammenhang mit dieser Formulierung kann ein Skalarprodukt für Funktionen
verwendet werden, wobei allerdings im Unterschied zu (13) eine der beiden Funktionen durch ihre komplex Konjugierte
zu ersetzen ist, bevor das Integral gebildet wird. Man spricht dann auch von einem inneren Produkt, um es sprachlich von der
reellen Version zu unterscheiden.
|
| | |

komplex konjugieren
| |
| | |
| Fourierreihe mit Periode L |
| | | |
Zum Seitenanfang | |
| | |
Bisher haben wir nur periodische Funktionen betrachtet, deren Periodenlänge
2π ist. Der gesamte Formalismus kann leicht
auf Funktionen übertragen werden, deren Periodenlänge durch irgendeine andere Zahl
L > 0 gegeben ist.
Die einfachste Methode, alle bisherigen Ergebnisse auf diesen allgemeinen Fall zu übertragen, besteht darin,
anstelle der gegebenen Funktion f mit
Periode L die Hilfsfunktion
zu betrachten. h besitzt die Periode
2π, denn
| h(x + 2π)
= f ( |
L x
2π |
+ L)
= |
f ( |
L x
2π |
)
= h(x) |
|
(44) |
für alle x. Nun wird h
in der bisher besprochenen Form in einer Fourierreihe entwickelt und danach alles wieder durch
f ausgedrückt. Alles in allem besteht der
allgemeinere Formalismus, der auf diese Weise erhalten wird, darin, dass einige der Faktoren
π der obigen Formeln durch
L/2 und die trigonometrischen Basisfunktionen durch
| 1 |
, |
cos ( |
2πnx
L |
) |
, |
sin ( |
2πnx
L |
) |
|
(45) |
ersetzt werden.
Die Fourierreihe mit Periode
L
lautet
| |
|
|
∞ |
|
| f (x)
= |
a0
2 |
+ |
∑ |
(
an |
cos ( |
2πnx
L |
) |
+
bn |
sin ( |
2πnx
L |
) |
) |
|
, |
| |
|
|
n
= 1 |
|
|
(46) |
wobei die Entwicklungskoeffizienten durch
| |
|
|
L/2 |
|
| a0
= |
2
L |
|
∫ |
|
f (x)
dx |
|
| |
|
|
–L/2 |
|
|
(47) |
sowie
| |
|
|
L/2 |
|
| an
= |
2
L |
|
∫ |
|
f (x) |
cos ( |
2πnx
L |
) |
dx |
|
| |
|
|
–L/2 |
|
|
(48) |
und
| |
|
|
L/2 |
|
| bn
= |
2
L |
|
∫ |
|
f (x) |
sin ( |
2πnx
L |
) |
dx |
|
| |
|
|
–L/2 |
|
|
(49) |
gegeben sind.
Die spektrale Form einer solchen Fourierreihe lautet
| |
|
|
∞ |
|
| f (x)
= |
A0
2 |
+ |
∑ |
An |
cos ( |
2πnx
L |
–
φn) |
|
, |
| |
|
|
n
= 1 |
|
|
(50) |
wobei die Umrechnung der Koeffizienten durch die gleichen Formeln
(36) – (38b) wie früher beschrieben wird.
Die komplexe Form der Fourierreihe lautet
| |
|
|
∞ |
|
| f (x)
= |
|
|
∑ |
|
cn e2πinx/L |
|
| |
|
|
n = –∞ |
|
|
(51) |
mit
| |
|
|
L/2 |
|
| cn
= |
1
L |
|
∫ |
|
f (x)
e–2πinx/L dx |
. |
| |
|
|
–L/2 |
|
|
(52) |
Der Zusammenhang mit den Koeffizienten in (46) ist durch die gleichen Formeln
(42a) – (42c) wie früher beschrieben.
In allen Formeln mit Integralen kann anstelle des Integrationsintervalls [–L/2, L/2]
kann auch jedes andere Intervall der Länge L genommen werden.
|
Wir können nun die Variable x physikalisch ganz korrekt als Zeit ansehen.
Die Periode L erhält dann die Bedeutung der Periodendauer
der Grundschwingung. In der Physik wird zur Beschreibung eines zeitlichen Ablaufs statt x das
Symbol t gewählt. Die Periodendauer
T, die das Symbol L
ersetzt, wird meist in einer der Formen
angeschrieben, womit die in der Fourierreihe auftretenden trigonometrischen Funktionen die Form
annehmen. ν wird Frequenz der Grundschwingung genannt (diesmal in korrekter
physikalischer Begrifflichkeit als Zahl der vollständigen Perioden pro Zeitintervall). Oft wird für diese
Größe auch das Symbol f verwendet, das wir aber für
die zu entwickelnde Funktion reserviert haben. ω ist die
so genannte Kreisfrequenz der Grundschwingung. Fourierreihen werden in der Akustik benutzt, um Töne und Klänge
zu analysieren. Das Amplitudenspektrum ist die für die Klangfarbe hauptverantwortliche Größe.
In der Elektrotechnik kommen Fourierreihen beispielsweise bei der Analyse des Verhaltens von elektrischen Impulsen in
Schaltkreisen zum Einsatz.
|
| | |
| |
| | |
| Kontinuierliche Verallgemeinerung: die Fouriertransformation |
| | | |
Zum Seitenanfang | |
| | |
Wir erwähnen zum Abschluss noch ein Konzept, das auf nicht-periodische Funktionen angewandt werden kann.
Können wir die Periode L immer größer machen,
so dass sie letzlich (im Grenzübergang
L → ∞)
mit ganz R übereinstimmt?
Das ist tatsächlich möglich: Für wachsendes L
wird die Größe 2πn/L, die in der
Fourierreihe mit Periode L auftritt, bei
festgehaltenem n immer kleiner. Die Differenz
zweier solcher benachbarter Größen
(für n und
n + 1) wird ebenfalls immer kleiner.
Im Grenzübergang L → ∞ wird
k = 2πn/L
daher zu einer kontinuierlichen Variable, und die Summe über
n in der Fourierreihe wird durch ein Integral
ersetzt. Damit erhalten wir so etwas wie die Entwicklung einer gegebenen (nicht-periodischen)
Funktion f in Schwingungen beliebiger Frequenzen
(also nicht nur in ganzzahlige Vielfache einer Grundfrequenz). Sie wird üblicherweise in komplexer Form angeschrieben
und lautet
| |
|
|
∞ |
|
| f (x)
= |
1
(2π)1/2 |
|
∫ |
|
F(k)
eikx dk |
. |
| |
|
|
–∞ |
|
|
(55) |
Die Funktion F spielt die Rolle der
Entwicklungekoeffizienten
cn in der komplexen Form der Fourierreihe.
Sie heißt Fouriertransformierte von f, und der
Übergang
f ↦ F heißt Fouriertransformation.
Besonders schön ist die Formel, mit der wir sie aus f
berechnen können. Sie ist die Entsprechung von (52) und
lautet
| |
|
|
∞ |
|
| F(k)
= |
1
(2π)1/2 |
|
∫ |
|
f (x)
e–ikx dx |
. |
| |
|
|
–∞ |
|
|
(56) |
Beachten Sie, dass sie eine ganz ähnliche Form wie (55) hat. Der Vorfaktor in (55)
wurde so gewählt, dass sich in (56) der gleiche Vorfaktor ergibt. Wenn Sie für eine Funktion
f die Funktion F
mit (56) berechnen und in (55) einsetzen, so erhalten Sie
f zurück. (Dabei ist vorausgesetzt, dass alle vorkommenden
Integrale existieren. Die Fouriertransformation ist nur für Funktionen, die im Unendlichen genügend
schnell gegen 0 gehen und im Endlichen keine allzu schlimmen Unendlichkeiten
besitzen, anwendbar).
In der Quantentheorie spielt k die
Rolle des Impulses (genauer: Impuls =
Plancksche Konstante mal k).
Die Fouriertransformation ist die mathematische Grundlage für die
Heisenbergsche Unschärferelation.
|
| | |

Grenzprozesse
| |