| | |
| | | |
| |
| | |
| | | |
| |
| | |
Wir wollen zu Beginn dieses zweiten Vektorkapitels auf zwei Voraussetzungen aufmerksam machen:
- Im ersten Vektorkapitel haben wir die elementaren Begrifflichkeiten der Vektoren sowie
die Multiplikation eines Vektors mit einem Skalar, die Vektoraddition und
den Betrag eines Vektors eingeführt. Wir werden diese Strukturen auch hier
benötigen.
- Für das Folgende ist es günstig, wenn Sie ein bisschen über Winkelfunktionen
- insbesondere über den Cosinus -
wissen. Falls die Winkelfunktionen nicht zu Ihrem Lernstoff gehören,
Sie den Stoff dieses Kapitel aber dennoch benötigen,
so ist das für den Großteil der hier besprochenen Dinge nicht allzu schlimm.
Die entscheidende Stelle, an der der Cosinus eines Winkels auftritt, ist Formel
(6).
Unterhalb der Begründung dieser Formel wird Ihnen eine "Umfahrung" angeboten,
mit deren Hilfe Sie das Wesentliche auch ohne Kenntnis der WInkelfunktionen verstehen können.
Die wenigen anderen Formeln, in denen Winkelfunktionen
(in Form der Ausdrücke
cos
 q
und
sin q
und
sin q)
vorkommen, können Sie einfach überspringen. q)
vorkommen, können Sie einfach überspringen.
Nach der von uns verwendeten Konvention werden Vektoren durch Fettdruck
gekennzeichnet. Zwischen Zeilen- und Spaltenvektoren wird nicht
unterschieden.
|
| | |

Vektoren 1
Winkelfunktionen
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Im ersten Vektorkapitel haben wir die grundlegenden Rechenoperationen für Vektoren
besprochen, die Multiplikation eines Vektors mit einem Skalar und die
Addition zweier Vektoren, und wir haben Vektoren geometrisch (als Pfeile) gedeutet.
In diesem Kapitel werden noch zwei weitere Operationen ("Produkte") dazukommen,
die wichtige geometrische Beziehungen zwischen Vektoren ausdrücken.
Der Umgang mit diesen Operationen wird leichter fallen,
wenn uns zusätzlich zur bisherigen Darstellung von Vektoren als Listen von Zahlen
(in Zeilen- oder Spaltenform angeschrieben) noch eine dritte zur Verfügung steht.
In gewisser Weise handelt es sich dabei um einen einfachen Trick.
Standardbasis für die Ebene
| | | |

Rechenoperationen
für Vektoren
| |
| | |
Betrachten wir zuerst zweikomponentige (ebene) Vektoren und sehen wir uns die folgende Umformung an:
| ⎛ |
5 |
⎞ |
= 5 |
⎛ |
1 |
⎞ |
+ 2 |
⎛ |
0 |
⎞ |
. |
| ⎝ |
2 |
⎠ |
⎝ |
0 |
⎠ |
⎝ |
1 |
⎠ |
|
(1) |
Dabei haben wir lediglich verwendet, dass die Multiplikation mit einem Skalar und die Vektoraddition
komponentenweise definiert sind. Die Zahlen 5 und
2, die Komponenten des Vektors, treten auf der rechten Seite
als Skalare auf. Das kann man natürlich mit jedem zweikomponentigen Vektor
machen, und wir führen für die Vektoren, die als Komponenten nur
0 und 1
haben, eigene Namen ein. Wir bezeichnen
| e1 = |
⎛ |
1 |
⎞ |
e2 = |
⎛ |
0 |
⎞ |
|
| ⎝ |
0 |
⎠ |
⎝ |
1 |
⎠ |
|
(2) |
als Basisvektoren. Sie sind beide Einheitsvektoren,
| e1|
= | e1|
= | e2| = 1,
und zeigen in die Richtung der
x- bzw. der y-Achse.
Daher werden sie manchmal auch als ex und
ey
geschrieben. Zusammen bilden sie ein System von zwei Vektoren, das als
Standardbasis (oder Koordinatenbasis) bezeichnet wird. Wir können den Vektor (1)
nun bequem in der Form
5e1 + 2e2
schreiben. (Wir sagen: er wird "in die Standardbasis entwickelt").
Der Sinn der Standardbasis besteht darin, einen beliebigen Vektor als Linearkombination
der Basisvektoren schreiben zu können. Die Komponenten des Vektors treten dabei als Koeffizienten auf. e2| = 1,
und zeigen in die Richtung der
x- bzw. der y-Achse.
Daher werden sie manchmal auch als ex und
ey
geschrieben. Zusammen bilden sie ein System von zwei Vektoren, das als
Standardbasis (oder Koordinatenbasis) bezeichnet wird. Wir können den Vektor (1)
nun bequem in der Form
5e1 + 2e2
schreiben. (Wir sagen: er wird "in die Standardbasis entwickelt").
Der Sinn der Standardbasis besteht darin, einen beliebigen Vektor als Linearkombination
der Basisvektoren schreiben zu können. Die Komponenten des Vektors treten dabei als Koeffizienten auf.
Standardbasis für den dreidimensionalen Raum
| | | |
| |
| | |
Für dreikomponentige (räumliche) Vektoren können wir dasselbe machen. Wir führen die
Basisvektoren
| e1 = |
⎛ |
1 |
⎞ |
e2 = |
⎛ |
0 |
⎞ |
e3 = |
⎛ |
0 |
⎞ |
|
| ⎜ |
0 |
⎟ |
⎜ |
1 |
⎟ |
⎜ |
0 |
⎟ |
| ⎝ |
0 |
⎠ |
⎝ |
0 |
⎠ |
⎝ |
1 |
⎠ |
|
(3) |
ein. Auch sie sind Einheitsvektoren,
| e1|
= | e1|
= | e2| = | e2| = | e3| = 1,
zeigen in die Richtung der
x-, y- bzw. der z-Achse
und können auch als ex,
ey
und ez
geschrieben werden. Zusammen bilden sie eine Standardbasis für den dreidimensionalen Raum.
Der Vektor e3| = 1,
zeigen in die Richtung der
x-, y- bzw. der z-Achse
und können auch als ex,
ey
und ez
geschrieben werden. Zusammen bilden sie eine Standardbasis für den dreidimensionalen Raum.
Der Vektor
lässt sich mit ihrer Hilfe bequem in der Form
3e1 - 2e2 + 4e3
schreiben. Eine analoge Konstruktion ist natürlich in jeder Dimension möglich.
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Eine wichtige Sache haben wir im Rahmen der Vektorrechnung und der geometrischen Deutung von Vektoren
noch nicht betrachtet: wir haben (noch) kein Maß für den Winkel, den
zwei Vektoren einschließen.
Wenden wir uns nun diesem Thema zu. Wir werden dabei eine ganz erstaunliche Entdeckung machen.
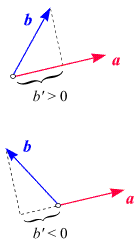 Interessanterweise ist der von zwei Vektoren eingeschlossenen Winkel gar nicht die günstigste
Kenngröße, wenn es um Winkelbeziehungen zwischen Vektoren geht!
Was dem Vektorbegriff näher steht, sind Längen. Eine Länge, die
etwas damit zu tun hat, wie zwei Vektoren "richtungsmäßig" zueinander stehen, ist in den beiden nebenstehenden
Skizzen dargestellt: Betrachten wir zwei Vektoren
a und b,
deuten sie als Pfeile (egal, ob in der Ebene oder im Raum) und hängen sie mit ihren Schäften
in einen beliebigen Punkt. Dann projizieren wir
b in die Richtung von a,
d.h. wir fällen eine Normale von der Spitze von b bis zu jener Geraden,
entlang der a liegt.
Dadurch entsteht eine Zahl b', die wir
Interessanterweise ist der von zwei Vektoren eingeschlossenen Winkel gar nicht die günstigste
Kenngröße, wenn es um Winkelbeziehungen zwischen Vektoren geht!
Was dem Vektorbegriff näher steht, sind Längen. Eine Länge, die
etwas damit zu tun hat, wie zwei Vektoren "richtungsmäßig" zueinander stehen, ist in den beiden nebenstehenden
Skizzen dargestellt: Betrachten wir zwei Vektoren
a und b,
deuten sie als Pfeile (egal, ob in der Ebene oder im Raum) und hängen sie mit ihren Schäften
in einen beliebigen Punkt. Dann projizieren wir
b in die Richtung von a,
d.h. wir fällen eine Normale von der Spitze von b bis zu jener Geraden,
entlang der a liegt.
Dadurch entsteht eine Zahl b', die wir
- als
positiv veranschlagen, wenn a und b
eine spitzen Winkel miteinander einschließen (obere Skizze)
- und als negativ, wenn a und b
eine stumpfen Winkel miteinander einschließen (untere Skizze).
Aufgrund dieser Vorzeichenkonvention wird b' auch
orientierte Projektion genannt.
Der Absolutbetrag von b' ist in jedem Fall
gleich der Länge der Projektion von b
auf a. Wir können uns diesen Projektionsprozess als
das Werfen eines Schattens vorstellen, wenn das Licht normal zu a
einfällt.
Mit dieser Größe b' machen wir nun etwas,
dessen weitreichende Konsequenzen erst in den nachfolgenden Schritten klar werden:
Geometrische Definition des Skalarprodukts
| | | |
| |
| | |
Wir definieren
das Skalarprodukt der Vektoren a und b
als
Manchmal wird es auch mit einem Punkt in der Form
angeschrieben. Seinen Namen trängt es, weil es aus zwei Vektoren einen Skalar, d.h.eine Zahl macht
(oder, anders ausgedrückt, aus zwei gerichteten Größen eine ungerichtete).
Es wird auch manchmal inneres Produkt genannt.
Sehen wir uns ein paar seiner Eigenschaften an. Drei Eigenschaften kennen wir schon, da sie unmittelbar aus seiner
Definition folgen:
- Es gilt a
 b
> 0 genau dann, wenn a und b
einen spitzen Winkel einschließen. b
> 0 genau dann, wenn a und b
einen spitzen Winkel einschließen.
- Es gilt a
 b
< 0 genau dann, wenn a und b
einen stumpfen Winkel einschließen. b
< 0 genau dann, wenn a und b
einen stumpfen Winkel einschließen.
- Es gilt a
 b
= 0 genau dann, wenn a und b
aufeinander normal stehen. b
= 0 genau dann, wenn a und b
aufeinander normal stehen.
Ist (zumindest) einer der beiden Vektoren 0, so
betrachten wir das als Spezialfall des dritten Punktes.
Nach dieser Konvention steht der Nullvektor auf jeden Vektor normal.
Der Zusammenhang zwischen dem Skalarprodukt und dem Winkel ist nun durch folgende Formel gegeben:
| | | |
| |
| | |
 wobei
q der von a
und b eingeschlossene Winkel ist.
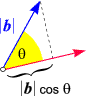
Wir können sie ganz leicht beweisen: Der nebenstehenden Skizze entnehmen wir
b' =
|
wobei
q der von a
und b eingeschlossene Winkel ist.
Wir können sie ganz leicht beweisen: Der nebenstehenden Skizze entnehmen wir
b' =
| b b |
cos |
cos q,
wobei wir uns erinnern, dass der Cosinus eine Winkels gerade durch eine solche Projektion definiert ist.
(Wenn es Ihnen lieber ist, können Sie auch den Merksatz
"Cosinus = Ankathete dividiert durch Hypotenuse" auf das rechtwinkelige Dreieck in der Skizze anwenden).
Diese Formel garantiert auch, dass
b' negativ ist, wenn a
und b einen stumpfen Winkel einschließen,
d.h. wenn q > 90°
ist. q,
wobei wir uns erinnern, dass der Cosinus eine Winkels gerade durch eine solche Projektion definiert ist.
(Wenn es Ihnen lieber ist, können Sie auch den Merksatz
"Cosinus = Ankathete dividiert durch Hypotenuse" auf das rechtwinkelige Dreieck in der Skizze anwenden).
Diese Formel garantiert auch, dass
b' negativ ist, wenn a
und b einen stumpfen Winkel einschließen,
d.h. wenn q > 90°
ist.
| | | |
Cosinus
| |
| | |
Falls Winkelfunktionen nicht zu Ihrem Lernstoff gehören,
klicken Sie auf den nebenstehenden Button für eine "Umfahrungsstraße",
um auch ohne Vorkenntnisse über Winkelfunktionen mit Formel (6)
etwas anfangen zu können.
Was noch fehlt, ist eine bequeme Berechnungsmethode für das Skalarprodukt. Und hier beginnen die Überraschungen: Zunächst
folgt aus (6), dass das Skalarprodukt symmetrisch ist, d.h. dass immer
a b
=
b b
=
b a a |
|
|
(7) |
gilt. Man könnte also genausogut a in die Richtung von
b projizieren und das Skalarprodukt mit vertauschten Rollen
der beiden Vektoren definieren - es ergibt sich dasselbe Resultat!
Nun können wir jene Rechengesetze für das Skalarprodukt formulieren, die uns zu einer einfachen Berechnungsmethode führen werden:
- Wird b durch ein Vielfaches, sagen wir
r
 b,
ersetzt, so wird auch b' durch das
r-fache ersetzt (siehe die Skizze links unten). Daher gilt
a b,
ersetzt, so wird auch b' durch das
r-fache ersetzt (siehe die Skizze links unten). Daher gilt
a (r (r b)
= r a b)
= r a b.
Aufgrund der Symmetrie (7) gilt auch
(r b.
Aufgrund der Symmetrie (7) gilt auch
(r a) a) b
= r a b
= r a b.
Mit anderen Worten: erscheint einer der beiden Vektoren mit einem Skalar multipliziert, so kann
dieser aus dem Skalarprodukt herausgezogen werden. b.
Mit anderen Worten: erscheint einer der beiden Vektoren mit einem Skalar multipliziert, so kann
dieser aus dem Skalarprodukt herausgezogen werden.
- Wird b durch eine Summe, sagen wir
b + c,
ersetzt so wird auch b' durch die
Summen der Projektionen b' + c'
ersetzt (siehe die Skizze rechts oben). Daher gilt
a
 (b + c)
= a (b + c)
= a b +
a b +
a c.
Aufgrund der Symmetrie (7) gilt auch immer
(a + b) c.
Aufgrund der Symmetrie (7) gilt auch immer
(a + b) c
= a c
= a c +
b c +
b c.
Mit anderen Worten: Das Skalarprodukt eines Vektors mit einer Summe ist die Summe der Skalarprodukte. c.
Mit anderen Worten: Das Skalarprodukt eines Vektors mit einer Summe ist die Summe der Skalarprodukte.
Diese beiden Eigenschaften gemeinsam besagen, dass mit Klammern ganz ähnlich umgegangen werden kann,
wie wir das von Zahlen gewohnt sind.
In mathematischen Fachbegriffen ausgedrückt heißt das, dass das Bilden des Skalarprodukts mit einem
gegebenen Vektor eine lineare Operation ist oder, was dasselbe bedeutet,
dass das Skalarprodukt eine bilineare ( = = in
beiden Vektoren lineare) Operation ist. in
beiden Vektoren lineare) Operation ist.
Nun sind wir bereit für die
Berechnung des Skalarprodukts
| | | |
| |
| | |
Erinnern wir uns an den ersten Abschnitt
dieses Kapitels, in dem wir Vektoren durch die Standardbasis
(2) für den ebenen und (3) für den räumlichen
Fall ausgedrückt haben. Behandeln wir zuerst ebene Vektoren.
Zwei zweikomponentige Vektoren a = (a1, a2)
und b = (b1, b2)
können mit Hilfe der Standardbasis in der Form
a = a1e1 + a2e2 und
b = b1e1 + b2e2
geschrieben werden. Bilden wir nun deren Skalarprodukt, so können wir es dank der soeben gefundenen
Rechenregeln "ausmultiplizieren" und erhalten
a b
=
a1b1 e1e1 +
(a1b2 + a2b1) e1e2 +
a2b2 e2e2 b
=
a1b1 e1e1 +
(a1b2 + a2b1) e1e2 +
a2b2 e2e2 |
. |
|
(8) |
Dabei haben wir auch gleich die Symmetrieeigenschaft (7) in der Form
e2e1 = e1e2
benutzt. Nun ist alles zurückgeführt auf die drei Skalarprodukte der
Basisvektoren untereinander. Da
e1 und
e2 aufeinander normal stehen, ist
e1e2 = 0.
Das Skalarprodukt von e1
mit sich selbst ergibt sich aufgrund der geometrischen Definition (5) und
zusammen mit der Tatsache, dass e1 ein Einheitsvektor ist, zu
e1e1 = 1,
und aus demselben Grund ist e2e2 = 1.
Setzen wir das in (8) ein. so erhalten wir die
Formel zur Berechnung des Skalarprodukts für ebene Vektoren:
a b
=
a1b1 +
a2b2 b
=
a1b1 +
a2b2 |
. |
|
(9) |
Ihre Einfachheit stellt die eigentliche Überraschung dar! Man multipliziere die beiden ersten Komponenten
und addiere das Produkt der beiden zweiten Komponenten - fertig!
In vielen Lehrbüchern wird das Skalarprodukt durch diese Formel definiert, und unsere ursprüngliche
Definition (5) sowie die Formel (6), die den Zusammenhang zum
Cosinus des eingeschlossenen Winkels herstellt, werden als Konsequenzen daraus abgeleitet.
In diesem Fall besteht die Überraschung darin, dass (9) eine einfache
geometrische Bedeutung hat.
Diese einfache geometrische Bedeutung bezieht sich überdies nur auf die relative Richtung der beiden Vektoren
zueinander, in keiner Weise aber auf die Koordinatenachsen.
Falls wir die Vektoren a und
b gemeinsam auf eine beliebige
Weise rotieren, so dass ihre Beträge und der von ihnen eingeschlossene Winkel gleich
bleiben, so werden die dadurch erhaltenen rotierten Vektoren, nennen wir sie
a' und b',
ganz andere Komponenten haben als
a und b.
Dennoch wird ihr Skalarprodukt, beide Male mit Formel (9) berechnet, das gleiche sein:
a b =
a' b =
a' b'.
Diese Eigenschaft der Formel (9) nennen wir Rotationsinvarianz. b'.
Diese Eigenschaft der Formel (9) nennen wir Rotationsinvarianz.
Für dreikomponentige Vektoren kann die Berechnung des Skalarprodukts in völlig analoger Weise
durchgeführt werden (Berechnen Sie zur Übung selbst den (8) entsprechenden Ausdruck!)
Es ergibt sich die
Formel zur Berechnung des Skalarprodukts für räumliche Vektoren:
a b
=
a1b1 + a2b2 +
a3b3 b
=
a1b1 + a2b2 +
a3b3 |
. |
|
(10) |
In höheren Dimensionen verlässt uns die Anschauung, aber wir sind frei,
das Skalarprodukt für n-komponentige
Vektoren durch die Formel
a b
=
a1b1 + a2b2 + ...
+ anbn b
=
a1b1 + a2b2 + ...
+ anbn |
|
|
(11) |
zu definieren.
Die Kombination aus einfacher Berechnung -
Formeln (9), (10) und (11) -
und geometrischer Bedeutung -
Formeln (5) und (6) -
macht das Skalarprodukt zu einem mächtigen Werkzeug der analytischen (d.h. "berechnenden")
Geometrie.
Im Folgenden wollen wir einige mit ihm in Zusammenhang stehende Themen anreißen.
Skalarprodukt und Betrag
| | | |
Analytische
Geometrie 1
| |
| | |
Das Skalarprodukt eines Vektors mit sich selbst,
a a,
das wir der Einfachheit halber als
a2
schreiben und "Quadrat des Vektors a" nennen
(ausgesprochen "a-Quadrat"),
ist gleich dem Quadrat seines Betrages: a,
das wir der Einfachheit halber als
a2
schreiben und "Quadrat des Vektors a" nennen
(ausgesprochen "a-Quadrat"),
ist gleich dem Quadrat seines Betrages:
Das folgt sowohl aus der
geometrischen Definition (5), da die orientierte Projektion gleich dem Betrag ist,
oder aus (6), da
q = 0
und daher
cos q = 1
ist, oder, für beliebige Dimensionen, aus (11) durch simples
Einsetzen. q = 1
ist, oder, für beliebige Dimensionen, aus (11) durch simples
Einsetzen.
Orthogonalität
| | | |
| |
| | |
Eine der wichtigsten Eigenschaften des Skalarprodukts besteht darin,
uns sofort zu sagen, wann zwei Vektoren aufeinander normal (orthogonal) stehen.
Wie bereits oben gleich nach der Definition des Skalarprodukts
vermerkt, gilt
a
und
b
stehen genau dann aufeinander normal, wenn
a b
= 0. b
= 0. |
|
|
(13) |
Wenn man will, kann man das sogar als formale Definition der Orthgonalität ansehen
(was insbesondere in höheren Dimensionen mangels geometrischer Anschauung günstig ist).
Die Orthogonalität zweier Vektoren kann abgekürzt in der Form
a ^ b
ausgedrückt werden.
Damit können wir sofort enscheiden, ob zwei gegebene Vektoren aufeinander normal stehen.
Aufgabe: Stehen die Vektoren
a = (3, 1)
und b = (2, -6)
aufeinander normal?
Lösung: Wir berechnen
a b
= (3, 1) · (2, -6)
=
3 × 2 + 1 × (-6) = 6 - 6 = 0,
daher lautet die Antwort "ja". b
= (3, 1) · (2, -6)
=
3 × 2 + 1 × (-6) = 6 - 6 = 0,
daher lautet die Antwort "ja".
Steht ein Vektor auf einen anderen Vektor, auf eine Gerade (oder im Raum auf eine Ebene) normal, so nennen wir
ihn Normalvektor (ein vielseitiger Begriff, der in verschiedenen Zusammenhängen benutzt wird).
Für ebene Vektoren gibt es eine bequeme Methode, Normalvektoren zu finden. Sie funktioniert nach dem folgenden
Schema:
| a = |
⎛ |
a1 |
⎞ |
n = |
⎛ |
-a2 |
⎞ |
|
| ⎝ |
a2 |
⎠ |
⎝ |
a1 |
⎠ |
|
(14) |
Ist a gegeben, so steht n
normal dazu. (n entsteht aus
a durch eine Drehung um
90° im Gegenuhrzeigersinn, daher haben a
und n denselben Betrag).
Sehen Sie sich das Schema genauer an:
n wird erhalten, indem
die Komponenten von a
vertauscht werden und danach die erste mit -1
multipliziert wird.
Zur Übung: Überprüfen Sie durch Rechnung, ob diese beiden Vektoren tatsächlich aufeinander
normal stehen! Was ergibt sich, wenn statt dessen die zweite Komponente mit -1
multipliziert wird?
Aufgabe: Man finde einen Normalvektor zu
a = (3, 1).
Lösung:
n = (-1, 3)
durch Anwendung von (14).
Zusatzaufgabe: Zeichnen Sie beide Vektoren und versuchen sie, ohne Zuhilfenahme des Skalarprodukts zu beweisen,
dass sie aufeinander normal stehen!
Anwendung auf lineare Gleichungen
| | | |
| |
| | |
Mit dem Begriff des Skalarprodukts ergibt sich auch die
Möglichkeit, mathematische Ausdrücke, die zunächst mit Geometrie
nichts zu tun haben müssen, in kompakter Schreibweise abzukürzen
und geometrisch zu interpretieren. Dabei spielt Orthogonalität oft die entscheidende Rolle.
Betrachten wir als Beispiel den Fall einer Gleichung in zwei Variablen:
Sind a und b
gegebene Zahlen, und soll
die Menge aller Lösungen (x, y)
der Gleichung
| | | |
| |
| | |
(eine so genannte homogene lineare Gleichung) gefunden werden, so können die Koeffizienten
a, b
und die Variablen
x, y
jeweils zu Vektoren zusammengefasst werden:
a = (a, b)
und
x = (x, y).
Mit Hilfe der Berechnungsformel (9)
kann Gleichung (15) auch in der Form
a x = 0 x = 0
|
|
|
(16) |
angeschrieben werden. Abgesehen davon, dass das eine kürzere Schreibweise ist,
kann der Sachverhalt, den sie darstellt, nun in geometrischen Begriffen interpretiert werden:
a und b werden
als Komponenten eines gegebenen ebenen Vektors a
gedeutet. Das Problem, alle Lösungen von Gleichung (15) zu finden,
wird damit zu einem geometrischen Problem:
Gesucht sind alle ebenen Vektoren x, für die
(16) gilt, d.h. die auf a
normal stehen. Klarerweise bildet die Menge all dieser Vektoren eine (auf a
normal stehende) Gerade durch den Ursprung. Damit ist die Lösungsmenge
gefunden, und sie kann graphisch dargestellt werden.
Übungsaufgabe: Benutzen Sie diese Technik, um die Lösungsmenge der Gleichung
2x + 3y = 0
graphisch darzustellen!
| | | |

homogene lineare Gleichung in mehreren Variablen
| |
| | |
Diese Herangehensweise klappt manchmal auch für etwas kompliziertere Gleichungen. Von besonderem
Interesse ist die inhomogene lineare Gleichung
wobei nun c ebenfalls vorgegeben ist.
Mit a = (a, b)
und x = (x, y)
nimmt sie die Form
a x = c x = c
|
|
|
(18) |
an. Für welche ebenen Vektoren x hat das Skalarprodukt
mit a den vorgegebenen Wert
c?
Wir können diese Frage beantworten, indem wir uns an die geometrische
Definition (5) des Skalarprodukts erinnern:
Lassen wir x
die Rolle von b
übernehmen, so ist
a x
= x' x
= x' | | a a |,
wobei x' die orientierte Projektion
von x in die Richtung von
a ist.
Sehen Sie sich nun die folgende Skizze an: |,
wobei x' die orientierte Projektion
von x in die Richtung von
a ist.
Sehen Sie sich nun die folgende Skizze an:
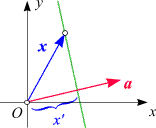
Alle Vektoren x,
für die x' einen vorgegebenen Wert
hat, liegen auf einer normal zu a
stehenden Geraden.
Wir können mit Hilfe der Vektorrechnung sogar den Abstand dieser Geraden vom Ursprung
berechnen: Stellen wir uns vor,
x0
ist der Ortsvektors jenes Punktes der Lösungsgeraden, der dem Ursprung am nächsten liegt.
Klicken Sie hier, um ihn in der obigen Skizze anzuzeigen!
Sein Betrag ist gleich dem gesuchten Abstand. Als Lösung von Gleichung (18)
erfüllt er
a x0 = c.
Weiters ist er parallel zu a,
daher ist das Skalarprodukt
a x0 = c.
Weiters ist er parallel zu a,
daher ist das Skalarprodukt
a x0
gemäß (5) oder (6) gleich dem Produkt der Beträge
| x0
gemäß (5) oder (6) gleich dem Produkt der Beträge
| a a | und
| | und
| x0 x0 | und
bekommt möglicherweise
(falls a und
x0 in entgegengesetzte Richtungen zeigen)
ein Minuszeichen. Setzen wir das in die Beziehung
a | und
bekommt möglicherweise
(falls a und
x0 in entgegengesetzte Richtungen zeigen)
ein Minuszeichen. Setzen wir das in die Beziehung
a x0 = c
ein und bilden auf beiden Seiten den Absolutbetrag, so ergibt sich
| x0 = c
ein und bilden auf beiden Seiten den Absolutbetrag, so ergibt sich
| a a |
| |
| x0 x0 |
=
| |
=
| c c |, was nach
| |, was nach
| x0 x0 |
aufgelöst zum gesuchten Abstand
| |
aufgelöst zum gesuchten Abstand
| x0 x0 |
=
| |
=
| c c |/| |/| a a |
führt.
Sehen wir uns die möglichen Vorzeichen des Skalarprodukts
a |
führt.
Sehen wir uns die möglichen Vorzeichen des Skalarprodukts
a x0
an, so erhalten wir als Nebenresultat: x0
zeigt in die gleiche Richtung wie a,
wenn c > 0
und in die entgegengesetzte Richtung, wenn c < 0
ist. x0
an, so erhalten wir als Nebenresultat: x0
zeigt in die gleiche Richtung wie a,
wenn c > 0
und in die entgegengesetzte Richtung, wenn c < 0
ist.
| | | |

inhomogene lineare Gleichung in mehreren Variablen
| |
| | |
In der ebenen analytischen Geometrie wird der Spieß umgedreht, und es werden Geraden durch Gleichungen der Form
(18) beschrieben. Ist eine Gerade in dieser Form gegeben, so
kann ein Normalvektor unmittelbar abgelesen werden: Es ist der Vektor
(a, b),
der aus den Koeffizienten der Gleichung gebildet wird.
Eine Gleichung der Form
a x = c
für dreikomponentige Vektoren beschreibt in ähnlicher Weise eine
Ebene im Raum, und wenn wir n-komponentige Vektoren
zulassen, können wir von einer
Hyperebene im R x = c
für dreikomponentige Vektoren beschreibt in ähnlicher Weise eine
Ebene im Raum, und wenn wir n-komponentige Vektoren
zulassen, können wir von einer
Hyperebene im R n
sprechen. n
sprechen.
Winkel zwischen zwei Vektoren
| | | |
Beschreibung von Geraden
Beschreibung
von Ebenen
| |
| | |
Sind zwei Vektoren a und b
gegeben, so kann der Cosininus des von ihnen eingeschlossenen Winkels unmittelbar aus (6)
gewonnen werden:
| | | |
| |
| | |
Der Winkel q selbst ergibt sich dann
(oft nur näherungsweise und mit Hilfe eines Rechners)
wie im Kapitel über die Winkelfunktionen besprochen durch Anwendung der "inversen Winkelfunktion"
Arcus-Cosinus. Er liegt im Bereich zwischen 0°
und 180° (im Bogenmaß: zwischen 0 und p). Betrachten
wir als Beispiel eine
Aufgabe: Welchen Winkel schließen die Vektoren
a = (3, 2)
und b = (4, -1) ein?
Lösung: Wir berechnen
a b
= (3, 2) · (4, -1)
=
3 × 4 + 2 × (-1) = 12 - 2 = 10.
Die Beträge der beiden Vektoren sind
| b
= (3, 2) · (4, -1)
=
3 × 4 + 2 × (-1) = 12 - 2 = 10.
Die Beträge der beiden Vektoren sind
| a a |
= 131/2
und
| |
= 131/2
und
| b b |
= 171/2. Mit (19) ist daher
cos |
= 171/2. Mit (19) ist daher
cos q
= 10/2211/2 » 0.672673,
und das exakte Resultat lautet:
q =
acos(10/2211/2).
Ein numerischer Näherungswert
ergibt sich unter Zuhilfenahme eines Rechners zu q »
0.832981 (oder, in Grad umgerechnet, 47.7263°). q
= 10/2211/2 » 0.672673,
und das exakte Resultat lautet:
q =
acos(10/2211/2).
Ein numerischer Näherungswert
ergibt sich unter Zuhilfenahme eines Rechners zu q »
0.832981 (oder, in Grad umgerechnet, 47.7263°).
Wenn Sie den Mini-Rechner
oder JavaCalc verwenden, so geben Sie für den letzten Schritt
acos(10/221^(1/2))
oder, wenn Sie das Resultat in Grad
ausgegeben haben wollen,
180/PI*acos(10/221^(1/2))
ein. Zeichnen Sie die beiden Vektoren und überprüfen Sie den berechneten Winkel, so genau es geht, mit dem Winkelmesser!
| | | |
inverse Winkelfunktionen
| |
| | |
Wie Sie anhand dieser Aufgabe sehen, gehört das Berechnen von Winkeln aus Vektoren
nicht unbedingt zu den angenehmsten Tätigkeiten, sollte aber im Prinzip keine Schwierigkeit darstellen.
Soll lediglich herausgefunden werden, ob zwei Vektoren einen spitzen oder stumpfen
Winkel miteinander einschließen (oder aufeinander normal stehen),
so können sie das, wie oben bemerkt, am Vorzeichen des
Skalarprodukts ablesen und ersparen sich das Berechnen der Beträge.
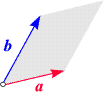
Parallelogrammfläche 1
Wir führen nun zwei Formeln an,
die Flächeninhalte betreffen. Betrachten wir zwei Vektoren
a
und b in der Ebene oder im Raum.
Hängen wir die ihnen entsprechenden Pfeile mit dem Schäften zusammen,
so spannen sie ein Parallelogramm auf (siehe Skizze).
Dessen Flächeninhalt A ist durch
| | | |
Parallelogramm
| |
| | |
gegeben. Im ebenen Fall reduziert sich diese Formel für a = (a1, a2)
und b = (b1, b2)
auf
A = | a1b2 - a2b1 a1b2 - a2b1 | | |
. |
|
(21) |
Wir werden ihr weiter unten im Zusammenhang mit dem zweiten "Produkt" für Vektoren noch einmal begegnen,
und daraus wird sich ein von diesem unabhängiger Beweis ergeben.
Skalarprodukt und Cosinussatz
| | | |
| |
| | |
Im Kapitel über Winkelfunktionen wird der so genannte Cosinussatz eingeführt. Er stellt eine Beziehung
zwischen Längen und Winkeln dar und wird für geometrische Berechnungen in Dreiecken
verwendet. Ohne auf Details einzugehen, wollen wir hier nur erwähnen, dass er in enger Beziehung zum
Skalarprodukt steht und mit seiner Hilfe recht elegant bewiesen werden kann.
Cauchy-Schwarzsche Ungleichung
| | | |
Cosinussatz
| |
| | |
Wir schreiben zum Abschluss dieses Abschnitts noch eine Ungleichung an, die für beliebige
Vektoren gilt:
Im ebenen und räumlichen Fall folgt sie daraus, dass der Cosinus in (6)
nie kleiner als -1
und nie größer als 1
sein kann, sie gilt aber in beliebigen Dimensionen. (Genau genommen beweist sie,
dass (6) in beliebigen Dimensionen dazu benutzt werden kann, um zu
definieren, was ein Winkel ist).
Das Skalarprodukt ist eine der nützlichsten Strukturen der gesamten Mathematik.
Wir werden insbesondere in den Kapiteln über die analytische Geometrie davon Gebrauch machen.
Es findet in praktisch allen physikalischen Theorien Anwendung.
In verallgemeinerter Form ist es zu einem Grundbaustein unseres physikalischen
Naturverständnisses, der Quantentheorie, geworden.
Wenn Sie viel mit ihm zu tun haben (werden), sollten sie mit allen seinen Aspekten, wie wir sie diskutiert haben,
gut vertraut sein, nicht nur mit den Berechnungsformeln (9) und (10).
|
| | |
| |
| | |
| | | |
Zum Seitenanfang | |
| | |
Wir haben ein zweites "Produkt" für Vektoren versprochen, und hier ist es.
Es trägt den Namen "Vektorprodukt" ist nur für
dreidimensionale (räumliche) Vektoren definiert. Im Unterschied zum Skalarprodukt
macht es aus zwei Vektoren einen dritten (daher auch sein Name).
Geometrische Definition des Vektorprodukts
| | | |
| |
| | |
Seien a und b
zwei räumliche Vektoren. Aus diesen beiden definieren wir einen Vektor namens
a Ù Ù b
(ausgesprochen: "a keil b") wie folgt: b
(ausgesprochen: "a keil b") wie folgt:
- a
 Ù Ù b
stehe normal auf a. b
stehe normal auf a.
- a
 Ù Ù b
stehe normal auf b. b
stehe normal auf b.
- Der Betrag von a
 Ù Ù b
sei gleich dem Flächeninhalt des Parallelogramms, das
a und b
aufspannen. b
sei gleich dem Flächeninhalt des Parallelogramms, das
a und b
aufspannen.
- Die bisherigen Forderungen bestimmen a
 Ù Ù b
bereits bis auf das Vorzeichen eindeutig. Letzteres legen wir durch die "Rechtsschraubenregel"
("Rechte-Hand-Regel") fest:
Drehen wir a auf kürzestem Weg in b
und denken uns diese beiden Vektoren mit einer Schraube verbunden, so zeigt
a b
bereits bis auf das Vorzeichen eindeutig. Letzteres legen wir durch die "Rechtsschraubenregel"
("Rechte-Hand-Regel") fest:
Drehen wir a auf kürzestem Weg in b
und denken uns diese beiden Vektoren mit einer Schraube verbunden, so zeigt
a Ù Ù b
in die Bewegungsrichtung der Schraube. b
in die Bewegungsrichtung der Schraube.
Der Vektor a Ù Ù b
heißt Vektorprodukt (oder vektorielles Produkt) von a und b.
Im Schulbereich wird er meist mit einem Kreuz × geschrieben
(a b
heißt Vektorprodukt (oder vektorielles Produkt) von a und b.
Im Schulbereich wird er meist mit einem Kreuz × geschrieben
(a × × b).
Man spricht deshalb auch vom Kreuzprodukt. Da wir das Kreuz aber gelegentlich für die
Multiplikation von Zahlen verwenden, und um Verwechslungen mit dem Buchstaben x vorzubeugen, ziehen
wir das Keilsymbol Ù vor.
Bisweilen findet sich auch der Name äußeres Produkt (der aber in der Regel eine andere, damit
verwandte Operation bezeichnet). b).
Man spricht deshalb auch vom Kreuzprodukt. Da wir das Kreuz aber gelegentlich für die
Multiplikation von Zahlen verwenden, und um Verwechslungen mit dem Buchstaben x vorzubeugen, ziehen
wir das Keilsymbol Ù vor.
Bisweilen findet sich auch der Name äußeres Produkt (der aber in der Regel eine andere, damit
verwandte Operation bezeichnet).
Dieses Produkt gehorcht interessanten Rechengesetzen:
| | | |
| |
| | |
- a
 Ù Ù a = 0,
d.h. das Vektorprodukt eines Vektors mit sich selbst ist der Nullvektor. Das folgt daraus, dass
in diesem Fall das Parallelogramm, von dem in Punkt 3 der Definition die Rede ist, zu einer
Linie kollabiert und daher den Flächeninhalt 0 besitzt. a = 0,
d.h. das Vektorprodukt eines Vektors mit sich selbst ist der Nullvektor. Das folgt daraus, dass
in diesem Fall das Parallelogramm, von dem in Punkt 3 der Definition die Rede ist, zu einer
Linie kollabiert und daher den Flächeninhalt 0 besitzt.
- a
 Ù Ù b =
- b =
- b b Ù Ù a,
d.h. unter einer Vertauschung von a und b
kehrt das Vektorprodukt seine Richtung um. (Wir nennen das Vektorprodukt daher auch antisymmetrisch).
Das folgt daraus, dass sich nach einem Rollentausch der beiden Vektoren die Schraube in Punkt 4
in die entgegengesetzte Richtung bewegt. a,
d.h. unter einer Vertauschung von a und b
kehrt das Vektorprodukt seine Richtung um. (Wir nennen das Vektorprodukt daher auch antisymmetrisch).
Das folgt daraus, dass sich nach einem Rollentausch der beiden Vektoren die Schraube in Punkt 4
in die entgegengesetzte Richtung bewegt.
- (r
 a) a) Ù Ù b =
a b =
a Ù Ù (r (r b) =
r a b) =
r a Ù Ù b, d.h.
ein Skalar r kann aus dem Vektorprodukt herausgezogen werden.
(Beweis: siehe nebenstehenden Button). b, d.h.
ein Skalar r kann aus dem Vektorprodukt herausgezogen werden.
(Beweis: siehe nebenstehenden Button).
-
a
 Ù Ù (b + c) =
a (b + c) =
a Ù Ù b +
a b +
a Ù Ù c
und
(a + b) c
und
(a + b) Ù Ù c =
a c =
a Ù Ù c +
b c +
b Ù Ù c,
d.h. das Vektorprodukt eines Vektors mit einer Summe ist die Summe der Vektorprodukte.
(Beweis: siehe nebenstehenden Button). c,
d.h. das Vektorprodukt eines Vektors mit einer Summe ist die Summe der Vektorprodukte.
(Beweis: siehe nebenstehenden Button).
- a
 Ù Ù 0 = 0,
d.h. das Vektorprodukt eines Vektors mit dem Nullvektor ergibt wieder den Nullvektor. 0 = 0,
d.h. das Vektorprodukt eines Vektors mit dem Nullvektor ergibt wieder den Nullvektor.
- a
 Ù Ù b
ist genau dann 0, wenn
a und
b zueinander parallel sind
(denn nur dann ist der Flächeninhalt des von ihnen aufgespannten Parallelogramms gleich 0). b
ist genau dann 0, wenn
a und
b zueinander parallel sind
(denn nur dann ist der Flächeninhalt des von ihnen aufgespannten Parallelogramms gleich 0).
| | | |
| |
| | |
Daraus folgt insbesondere, dass mit Klammern ganz ähnlich umgegangen werden kann,
wie wir das von Zahlen gewohnt sind.
In mathematischen Fachbegriffen ausgedrückt heißt das, dass das Bilden des Vektorprodukts mit einem
gegebenen Vektor eine lineare Operation ist oder, was dasselbe bedeutet,
dass das Vektorprodukt eine bilineare ( = = in
beiden Vektoren lineare) Operation ist. in
beiden Vektoren lineare) Operation ist.
Aber Achtung: Das Assoziativgesetz gilt nicht. Im Allgemeinen ist
a Ù Ù (b (b Ù Ù c)
¹
(a c)
¹
(a Ù Ù b) b) Ù Ù c. c.
Berechnung des Vektorprodukts
| | | |
| |
| | |
Nun haben wir genug Informationen gesammelt, um das Vektorprodukt berechnen zu können.
Wir gehen genauso vor wie im Fall des Skalarprodukts oben:
Durch die Standardbasis (3) ausgedrückt, können die Vektoren
a = (a1, a2, a3)
und b = (b1, b2, b2)
in der Form
a = a1e1 + a2e2 + a3e3 und
b = b1e1 + b2e2 + b3e3
geschrieben werden. Bilden wir deren Vektorprodukt, so können wir die soeben gefundenen
Rechenregeln verwenden, um es "auszumultiplizieren". Dabei benutzen wir, dass
das Vektorprodukt eines Vektors mit sich selbst 0
ist und weiters die Antisymmetrie (so ersetzen wir
e2 Ù Ù e1
durch
- e1
durch
- e1 e1 Ù Ù e2).
Um die verbleibenden Vektorprodukte der Basisvektoren zu ermitteln, kehren wir zur Definition
zurück und erhalten e2).
Um die verbleibenden Vektorprodukte der Basisvektoren zu ermitteln, kehren wir zur Definition
zurück und erhalten
e1 Ù Ù e2 = e3,
e2 e2 = e3,
e2 Ù Ù e3 = e1
und
e3 e3 = e1
und
e3 Ù Ù e1 = e2 . e1 = e2 . |
|
(23) |
Um die erste dieser Beziehungen zu beweisen, drehen Sie die positive x-Achse auf kürzestem
Weg in die positive y-Achse. Dann bewegt sich die "Schraube" in die
z-Richtung. Berücksichtigen wir noch,
dass e1 und
e2 aufeinander normal stehende
Einheitsvektoren sind, so ergibt sich
e1 Ù Ù e2
= e3. Die anderen Produkte ergeben sich auf analoge Weise.
Damit erhalten wir e2
= e3. Die anderen Produkte ergeben sich auf analoge Weise.
Damit erhalten wir
a Ù Ù b
= (a2b3 -
a3b2) b
= (a2b3 -
a3b2) e1
+ e1
+ |
(a3b1 -
a1b3) e2
+ (a1b2 -
a2b1) e2
+ (a1b2 -
a2b1) e3 , e3 , |
|
(24) |
womit das Berechnungsproblem im Prinzip gelöst ist. Ähnlich wie im Fall des Skalarprodukts
- siehe (9) und (10) -
ergibt sich eine erstaunlich einfache Formel. In Komponenten aufgeschrieben, lautet sie
a Ù Ù b = b =
|
⎛ |
a2b3
- a3b2 |
⎞ |
. |
| ⎜ |
a3b1
- a1b3 |
⎟ |
| ⎝ |
a1b2
- a2b1 |
⎠ |
|
(25) |
| | | |
| |
| | |
Um sich nicht alle Details dieser Formel auswendig merken zu müssen, können Sie nach folgendem Rezept vorgehen:
Zunächst wird übereingekommen, jedem
2 ×2-Zahlenschema
(jeder 2 ×2-Zahlenschema
(jeder 2 ×2-Matrix)
folgende Zahl (Determinante) zuzuordnen: ×2-Matrix)
folgende Zahl (Determinante) zuzuordnen:
| ⎛ |
r |
s |
⎞ |
® r u
- s u
- s t. t. |
| ⎝ |
t |
u |
⎠ |
|
(26) |
Dann schreiben Sie die beiden Vektoren als Spalten nebeneinander, wodurch ein
3 ×2-Zahlenschema
entsteht: ×2-Zahlenschema
entsteht:
| ⎛ |
a1 |
⎞ |
Ù |
⎛ |
b1 |
⎞ |
| ⎜ |
a2 |
⎟ |
⎜ |
b2 |
⎟ |
| ⎝ |
a3 |
⎠ |
⎝ |
b3 |
⎠ |
|
(27) |
Das Rezept lautet nun:
- Um die erste Komponente des Vektorprodukts zu ermitteln, decken Sie die erste Zeile
des obigen Zahlenschemas zu und ermitteln die Determinante der verbleibenden
2
 ×2-Matrix. ×2-Matrix.
- Um die zweite Komponente des Vektorprodukts zu ermitteln, decken Sie die zweite Zeile
des obigen Zahlenschemas zu, ermitteln die Determinante der verbleibenden
2
 ×2-Matrix
und multiplizieren sie mit -1. ×2-Matrix
und multiplizieren sie mit -1.
- Um die dritte Komponente des Vektorprodukts zu ermitteln, decken Sie die dritte Zeile
des obigen Zahlenschemas zu und ermitteln die Determinante der verbleibenden
2
 ×2-Matrix. ×2-Matrix.
Damit lassen sich Vektorprodukte fast so einfach ausrechnen wie Skalarprodukte.
Beispiel: Seien
a = (2, 4, 1) und
b = (3, -2, 1).
Wenden Sie die soeben besprochene Methode an, und Sie werden das Resultat
a Ù Ù b
= (6, 1, -16)
erhalten. b
= (6, 1, -16)
erhalten.
Zusatzaufgabe: Überzeugen Sie sich (durch Rechnung) davon, dass
a Ù Ù b
tatsächlich auf a und b
normal steht. b
tatsächlich auf a und b
normal steht.
Das Vektorprodukt kann eingesetzt werden, wenn es darum geht, den Normalvektor zu zwei gegebenen Vektoren zu
finden. Es lässt sich aber auch für Volumsberechnungen
verwenden und hängt mit den Begriffen "links" und "rechts" zusammen.
Spatprodukt, Volumen, lineare Abhängigkeit und Händigkeit
| | | |
Matrix
Determinante
(in Vorbereitung)
| |
| | |
Seien a, b und
c drei räumliche Vektoren. Dann bezeichnen wir die
Zahl
als deren Spatprodukt. (Beachten Sie die Struktur dieses Ausdrucks: Zuerst wird der Vektor
a Ù Ù b
gebildet und dann dessen Skalarprodukt mit c.
Das Resultat ist ein Skalar, d.h. eine Zahl). Mit ihm sind einige interessante
geometrische Themen verbunden: b
gebildet und dann dessen Skalarprodukt mit c.
Das Resultat ist ein Skalar, d.h. eine Zahl). Mit ihm sind einige interessante
geometrische Themen verbunden:
Der von drei Vektoren a, b und
c "aufgespannte" Körper (die dreidimensionale Verallgemeinerung des
Parallelogramms) heißt Parallelepiped. (Ein Spezialfall dafür ist der
Quader, falls die drei Vektoren paarweise aufeinander normal stehen).
Der Volumsinhalt V dieses Parallelepipeds
ist durch
| | | |
| |
| | |
gegeben, d.h. durch den Absolutbetrag des Spatprodukts.
Das Spatprodukt (28) dreier Vektoren ist genau dann 0, wenn
das Volumen des von ihnen aufgespannten Parallelepipeds 0
ist. Das ist der Fall, wenn die drei Vektoren (als Ortsvektoren aufgefasst) in einer Ebene liegen,
d.h. linear abhängig (koplanar) sind.
Daraus ergibt sich eine schnell anwendbare Methode, die lineare (Un-)Abhängigkeit
dreier gegebener Vektoren zu überprüfen. (Ihren Komponenten muss man sie
nicht unbedingt ansehen).
Aufgabe: Sind die drei Vektoren
a = (3, 2, 1),
b = (13, -2, -7) und
c = (-2, 4, 5)
linear abhängig oder unabhängig?
Lösung: Mit Hilfe der Formel (25) oder des Verfahrens (27)
berechnen Sie
a Ù Ù b
= (-12, 34, -32).
Das Skalarprodukt dieses Vektors mit c
errechnet sich unter Verwendung von (10) zu 0.
Daher sind die drei Vektoren linear abhängig. b
= (-12, 34, -32).
Das Skalarprodukt dieses Vektors mit c
errechnet sich unter Verwendung von (10) zu 0.
Daher sind die drei Vektoren linear abhängig.
Sind drei Vektoren linear unabhängig, so ist das Spatprodukt entweder
gleich V
oder -V,
je nach der Reihenfolge, in der sie angegeben werden.
Wir nennen die Eigenschaft, die für das Vorzeichen des Spatprodukts verantwortlich ist.
"Orientierung" oder "Händigkeit":
| | | |

linear (un-)abhängig
koplanar
| |
| | |
- Wir bezeichnen das System der drei Vektoren a, b und
c (in dieser Reihenfolge) als Rechtssystem oder rechtshändiges System,
wenn das Spatprodukt (28) positiv ist. Das ist der Fall, wenn
a
 Ù Ù b
und c einen spitzen Winkel bilden.
Ein Beispiel ist die Standardbasis (3).
Ganz allgemein bilden a,
b und
a b
und c einen spitzen Winkel bilden.
Ein Beispiel ist die Standardbasis (3).
Ganz allgemein bilden a,
b und
a Ù Ù b
ein Rechtssystem, sofern a und
b nicht parallel sind. b
ein Rechtssystem, sofern a und
b nicht parallel sind.
- Wir bezeichnen das System der drei Vektoren a, b und
c (in dieser Reihenfolge) als Linkssystem oder linkshändiges System,
wenn das Spatprodukt (28) negativ ist. Das ist der Fall, wenn
a
 Ù Ù b
und c einen stumpfen Winkel
bilden. b
und c einen stumpfen Winkel
bilden.
Aufgrund dieser Vorzeichenmöglichkeiten wird das Spatprodukt auch als
"orientierter Volumsinhalt" bezeichnet.
Die moderne Elementarteilchenphysik benutzt eine ganz ähnliche Struktur, um die Frage zu
thematisieren, ob die Naturgesetze zwischen "links" und "rechts" unterscheiden.
Aufgabe: Man stelle fest, ob es sich beim System
a = (1, 2, 1),
b = (3, -2, -3) und
c = (-2, 1, 2)
um ein Rechts- oder Linkssystem handelt und berechne das Volumen des von ihnen aufgespannten Parallelepipeds.
Lösung: Mit Hilfe der Formel (25) oder des Verfahrens (27)
berechnen Sie
a Ù Ù b
= (-4, 6, -8).
Das Skalarprodukt dieses Vektors mit c
errechnet sich unter Verwendung von (10) zu -2,
ist also negativ. Daher bilden die drei Vektoren (in der angegebenen Reihenfolge)
ein Linkssystem. Das Volumen des von ihnen aufgespannten Parallelepipeds ist 2. b
= (-4, 6, -8).
Das Skalarprodukt dieses Vektors mit c
errechnet sich unter Verwendung von (10) zu -2,
ist also negativ. Daher bilden die drei Vektoren (in der angegebenen Reihenfolge)
ein Linkssystem. Das Volumen des von ihnen aufgespannten Parallelepipeds ist 2.
Da durch Vertauschung zweier Vektoren ein Rechts- zu einem Linkssystem wird
(und umgekehrt), ändert sich die Händigkeit eines Systems
nach zwei solchen Vertauschungen nicht. Das gilt insbesondere für die
"zyklische Ersetzung"
a ®
b ®
c ® a,
die durch zwei Vertauschungen entsteht. Daraus folgt, dass das
Spatprodukt zyklisch ist, d.h. dass immer
gilt.
Parallelogrammfläche 2
| | | |
System
| |
| | |
Wir kommen nun zum zweiten Mal (vgl. oben) auf die Fläche des Parallelogramms
zu sprechen. Das Vektorprodukt ist zwar nur für räumliche Vektoren
definiert, aber mit Hilfe eines Tricks kann es auch für ebene Probleme genutzt
werden. Wenn wir nämlich die Zeichenebene mit der
xy-Ebene des Raumes
identifizieren, so kann jeder dreikomponentige Vektor, dessen dritte Komponente
0 ist, als ebener Vektor
aufgefasst werden. Seien
a = (a1, a2, 0)
und
b = (b1, b2, 0)
zwei solche Vektoren. Wie aus der Definition des Vektorprodukts folgt, zeigt
a Ù Ù b
in die z-Richtung. Mit
(25) ergibt sich sofort b
in die z-Richtung. Mit
(25) ergibt sich sofort
a Ù Ù b = b =
|
⎛ |
0 |
⎞ |
. |
| ⎜ |
0 |
⎟ |
| ⎝ |
a1b2
- a2b1 |
⎠ |
|
(31) |
Der Betrag dieses Vektors ist definitionsgemäß gleich dem Flächeninhalt des von
a und
b (in der
xy-Ebene) aufgespannten Parallelogramms.
Es ergibt sich für ihn daher genau die Formel (21),
die wir bereits auf andere Weise bewiesen haben.
Der Ausdruck
a1b2
- a2b1
kann für beliebige ebene Vektoren gebildet werden. Er ist eine Art ebenes Analogon
des Spatprodukts (28):
- Er ist genau dann 0,
wenn a und b
parallel, d.h. linear abhängig (kollinear) sind.
- Er ist genau dann positiv, wenn a und b nicht parallel sind und
die kürzeste Drehung von a in
b im Gegenuhrzeigersinn erfolgt.
Ein Beispiel ist die Standardbasis (2).
- Er ist genau dann negativ, wenn a und b nicht parallel sind und
die kürzeste Drehung von a in
b im Uhrzeigersinn erfolgt.
Einige Formeln zum Abschluss
| | | |
| |
| | |
Der Vollständigkeit halber erwähnen wir noch einige Identitäten für das Vektorprodukt.
Die ersten beiden lauten:
| | | |
| |
| | |
Sie folgen direkt aus der Definition des Vektorprodukts
(a Ù Ù b
steht normal auf a und b).
Weiters ist der Betrag des Vektorprodukts durch b
steht normal auf a und b).
Weiters ist der Betrag des Vektorprodukts durch
gegeben, wobei q der von
a und b
eingeschlossene Winkel ist.
Das ist gleichzeitig eine weitere Formel für den Flächeninhalt des Parallelogramms.
Eine letzte interessante Beziehung, die wir ohne Beweis angeben, ist
Sie zeigt uns, dass zwei aufeinanderfolgende Vektorprodukte durch das Skalarprodukt ausgedrückt
werden können.
Als ergänzende Literatur empfehlen wir das Vorlesungsskriptum
Vektorrechnung (PDF-Datei, von M. A. Knus, ETH Zürich).
|
| | |
| |