|
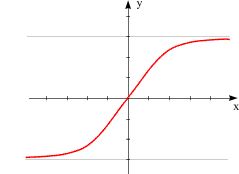
Die Funktion |
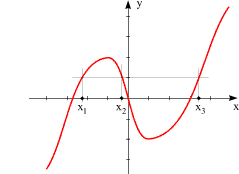
Die Funktion |
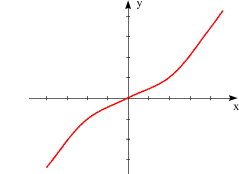
Die Funktion |
|
|
|
|
ist injektiv, aber nicht surjektiv. Ihr Wertebereich ist das (offene) Intervall |
ist surjektiv, aber nicht injektiv. So gibt es drei x-Werte (sie sind eingezeichnet), deren Funktionswert 1 ist. |
ist bijektiv, d.h. injektiv und surjektiv. |