|
3.1 Länge des Kreisbogens
|

  
|
Wir betrachten folgendes Bild:
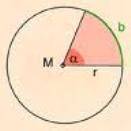 Bezeichnungen:
b... Kreisbogen
r... Radius
M... Mittelpunkt
α... Zentriwinkel (hängt von der Länge des Kreisbogens ab)
Wir wollen nun eine Formel finden, wie wir die Länge des Kreisbogens berechnen können:
α = 360° (Vollkreis; Bogen = Umfang) u = 2r·π
α = 1° Bogenlänge beträgt den 360. Teil
des Kreisumfangs 2r·π
b = ------
360
α° Bogenlänge ist αmal so groß
wie die Bogenlänge bei 1° 2r·π·α
b = --------
360
Nun erledige deinen 3. Arbeitsauftrag:
3. Arbeitsauftrag
Bezeichnungen:
b... Kreisbogen
r... Radius
M... Mittelpunkt
α... Zentriwinkel (hängt von der Länge des Kreisbogens ab)
Wir wollen nun eine Formel finden, wie wir die Länge des Kreisbogens berechnen können:
α = 360° (Vollkreis; Bogen = Umfang) u = 2r·π
α = 1° Bogenlänge beträgt den 360. Teil
des Kreisumfangs 2r·π
b = ------
360
α° Bogenlänge ist αmal so groß
wie die Bogenlänge bei 1° 2r·π·α
b = --------
360
Nun erledige deinen 3. Arbeitsauftrag:
3. Arbeitsauftrag 
Lernstoff, Übungsaufgabe, Eintrag in das Schulübungsheft
|
|
3.3 Übungen
|

 

|
Folgende drei Aufgaben sind zu erledigen:  1. Aufgabe:
Erledige das Rätsel zum Thema Kreisbogen und Flächeninhalt des Kreissektors:
Rätsel
2. Aufgabe:
-Zeichne in GeoGebra zwei verschiedene Kreissektoren.
-Beschrifte die Kreissektoren so, wie du es gelernt hast.
-Berechne die Zentriwinkel und Radien mit Hilfe von Geogebra.
-Berechne dann die Bogenlängen und die Flächeninhalte der Kreissektoren.
-Speicher die GeoGebra Datei ab und schreibe deine durchgeführten Rechnungen ins Schulübungsheft.
3. Aufgabe:
5. Arbeitsauftrag
1. Aufgabe:
Erledige das Rätsel zum Thema Kreisbogen und Flächeninhalt des Kreissektors:
Rätsel
2. Aufgabe:
-Zeichne in GeoGebra zwei verschiedene Kreissektoren.
-Beschrifte die Kreissektoren so, wie du es gelernt hast.
-Berechne die Zentriwinkel und Radien mit Hilfe von Geogebra.
-Berechne dann die Bogenlängen und die Flächeninhalte der Kreissektoren.
-Speicher die GeoGebra Datei ab und schreibe deine durchgeführten Rechnungen ins Schulübungsheft.
3. Aufgabe:
5. Arbeitsauftrag
Übungsaufgaben, Selfchecking Test
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



