|
1.1 Einleitung
|

 
|
Bevor du dich mit Wahrscheinlichkeit beschäftigst, ist es wichtig, dass du dich mit diesem Thema auseinandergesetzt und alles verstanden hast.
|
|
1.2 Erstes Beispiel
|

  
|
Um zu verstehen was mit diesem Begriff eigentlich gemeint ist, sehen wir uns dazu ein kleines Beispiel an:
Lege drei unterschiedliche Farbstifte vor dich auf den Tisch (zB.: grün, rot, blau).

Überlege, in welcher anderen Reihenfolge du die Stifte noch hinlegen kannst.
Zum Beispiel rot, grün, blau:

Wie viele verschiedene Möglichkeiten gibt es?
Lösung
|
|
1.3 Die Fakultät
|

 
|
Lege nun noch einen weiteren Stift in einer anderen Farbe dazu.
Du wirst feststellen, dass die Möglichkeiten, deine Stifte zu legen rasch mehr werden.
(hier sind es schon 24)
Zum Glück hat man bereits herausgefunden, wie man sich diese Anzahl von Möglichkeiten ganz schnell ausrechnen kann, ohne jede einzelne davon auszuprobieren.
Es ist eine Art von Wachstum, welche sich Fakultät nennt und man schreibt „ ! “.
Zum Beispiel mit drei Stiften: 3! = 3 · 2 · 1 = 6 Möglichkeiten
4 Stifte: 4! = 4 · 3 · 2 · 1 = 24 Möglichkeiten
Du siehst also dass du immer die Anzahl von Stiften, die du hast, multiplizieren musst − und zwar mit allen Zahlen die um eins kleiner sind als die vorangehende. (bis du bei 1 angelangt bist)
wichtig: 1! = 1, 0! = 1
Würdest du versuchen alle Möglichkeiten bei 10 Stiften auszuprobieren, wäre das eine lange Arbeit da: 10! = 10 · 9 · 8 · 7 · 6 · 5 · 4 · 3 · 2 · 1 = 3 628 800 Möglichkeiten
Versuche dieses Beispiel selbst, ohne Taschenrechner, zu lösen: 5! Lösung
|
|
1.4 "n über k"
|

 
|
Die Fakultät wirst du in der Wahrscheinlichkeitsrechnung brauchen, da es oft mehrere Möglichkeiten geben wird, die Lösung einer Frage zu finden, die du alle berücksichtigen musst.
Gehen wir nun einen Schritt weiter:
Nimm dir 10 verschiedene Stifte, tu sie in eine Schachtel und hole, ohne hinzusehen, 3 davon heraus.
Du hast nun 120 verschiedene Möglichkeiten, welche drei Stifte du in der Hand hast.
Man sagt: Die Anzahl an möglichen Ziehungen ist 120, oder: deine Chance genau die Stifte rot, grün und blau zu ziehen steht 1 zu 120.
Zu diesem Ergebnis kommen wir mithilfe einer Formel:
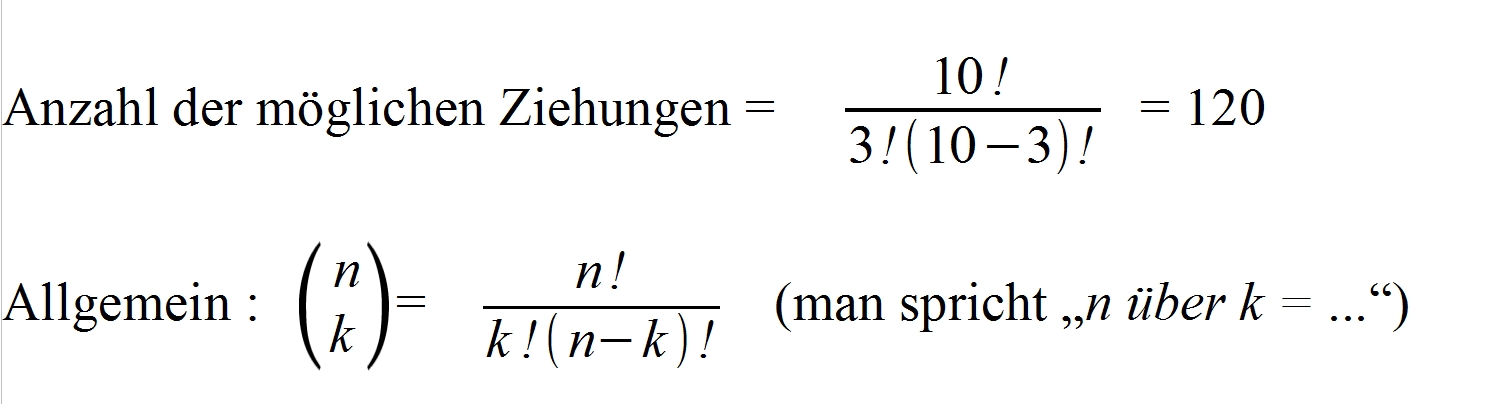
n ist hier die Anzahl aller vorhandenen Stifte und k die Menge an Stiften die gezogen wird.
In unserem Fall ist also n = 10 und k = 3.
Merke dir diese Formel, oder tippe
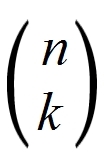 direkt in den Taschenrechner, falls du das gelernt hast.
direkt in den Taschenrechner, falls du das gelernt hast.
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



