|
4.1 Einleitung
|

 
|
Die Binomialverteilung ist ein sehr großes Kapitel, von dem wir hier allerdings nur die grundlegenden Dinge machen werden. Sie ist eine besondere Art von Verteilung, also werden wir erst einmal diese betrachten:
|
|
4.2 Verteilung und Erwartungswert
|

  
|
Eine Verteilung sieht zum Beispiel so aus:

Offensichtlich wird hier gewürfelt.
Würfelt man eine 6, 5 oder 4, dann gewinnt man Geld.
Würfelt man die 3, passiert nichts.
Bei einer 2 oder 1 muss man jedoch zahlen und verliert also Geld.
Nun können wir uns zum Beispiel überlegen, ob dieses Spiel gerecht ist.
Dazu lernen wir den Erwartungswert kennen:

Das heißt soviel, wie: Spielt man dieses Spiel verliert man im Durchschnitt 1/6 €, also circa 16 Cent.
Man spricht auch von einem für den Spieler ungünstigen Spiel.
Wie kann man nun das Spiel fair machen? - Man muss den Erwartungswert E = 0 setzen. Das funktioniert, indem man die Gewinne auf irgendeine Art verändert.
Wir können zum Beispiel festlegen, dass man nur 5 € verliert, wenn 1 gewürfelt wird:

Damit ist die Wahrscheinlichkeit dass man Geld verliert gleich groß, wie die, dass man Geld gewinnt.
Kann man aber im Durchschnitt mehr Geld gewinnen als verlieren ist das Spiel günstig.

Überlege selbst: Wie kannst du die Tabelle verändern, dass ein für den Spieler günstiges Spiel entsteht?
Lösung
|
|
4.3 Selbsterarbeitung
|

 

|
Zur Verteilung gibt es natürlich noch ein paar Dinge zu sagen, die wir hier überspringen werden.
Selbsterarbeitung:
Erarbeite dir mithilfe der zur Verfügung gestellten Seiten und deinem Buch folgende Begriffe selbst:
Varianz, Standardabweichung
Zur Verfügung gestellte Links:
Erwartungswert und Varianz
Erwartungswert, Varianz, Standardabweichung
Hilfe
|
|
4.4 Binomialverteilung, Bernoulli Experiment
|

  
|
Die Binomialverteilung zeichnet sich dadurch aus, dass jedes Spiel, Experiment oder Durchgang nur zwei Arten von Ausgängen hat:
Erfolg oder Misserfolg
Zum Beispiel zählt das Würfeln NICHT zur Binomialverteilung da es 6 verschiedene Ausgänge gibt. Allerdings können wir durch Einschränken eine Binomialverteilung erreichen:
Legen wir fest, das Würfeln einer 6 ist ein Erfolg, ansonsten ist es ein Misserfolg.
Man sagt: die Wahrscheinlichkeit auf Erfolg ist p = 1/6
p ist eine Abkürzung aus dem Englischen: probability = Wahrscheinlichkeit
Ein anderes Beispiel ist der Münzwurf:
Hier sind Erfolg und Misserfolg eindeutig: Zahl oder nicht Zahl.
Die Wahrscheinlichkeiten kennen wir bereits:
Erfolg: Zahl mit p = 0,5
Misserfolg: Kopf mit p = 0,5
Ein solches Experiment wie der Münzwurf mit 2 Ausgängen nennt man Bernoulli Experiment . Man kann natürlich, wie bereits gelernt, auch mehrere Durchgänge machen, was zu einer Bernoulli-Kette führt. Diese kann auch sehr schön gezeichnet werden:
Beispiel mit 3 fachem Münzwurf:
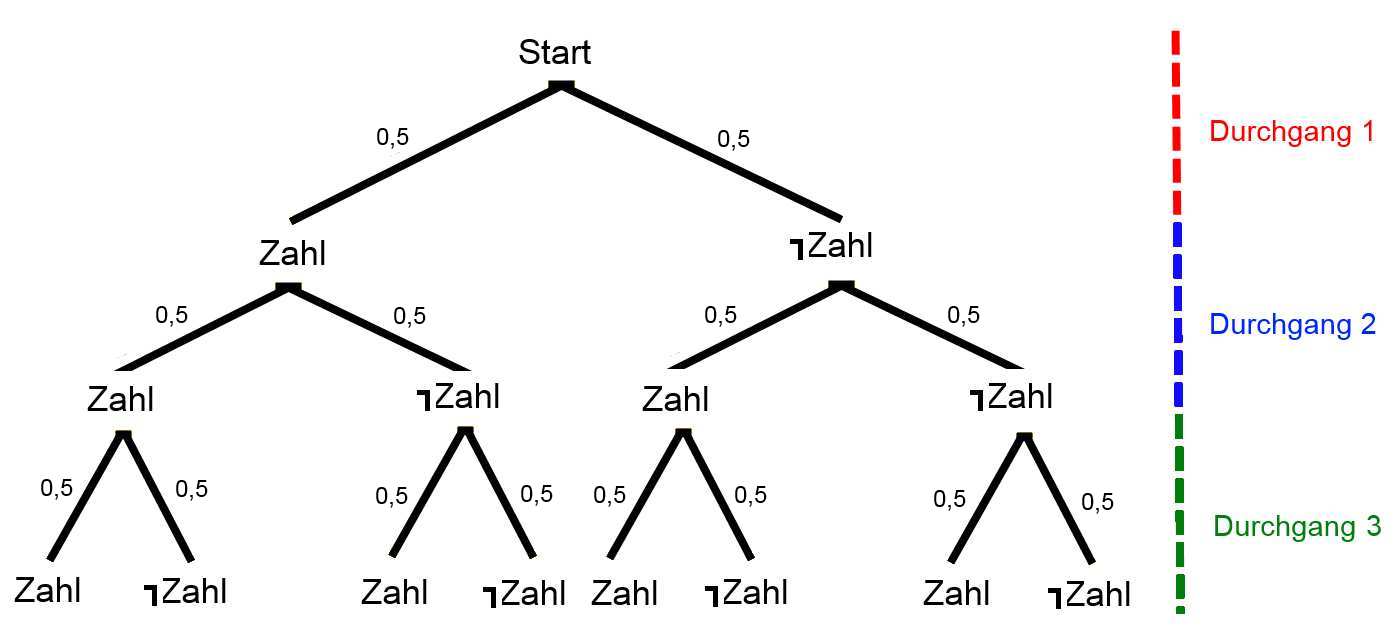
0,5 bezeichnet hier immer die jeweilige Wahrscheinlichkeit, mit der das Ereignis Zahl oder Nicht-Zahl eintritt.
Achtung diese Wahrscheinlichkeiten sind nicht immer gleich! Hier könnte ebenso an einem Ast 0,7 und am anderen 0,3 stehen.
Wie groß ist nun die Wahrscheinlichkeit, bei dreimal werfen genau zweimal Zahl und einmal Kopf zu haben?
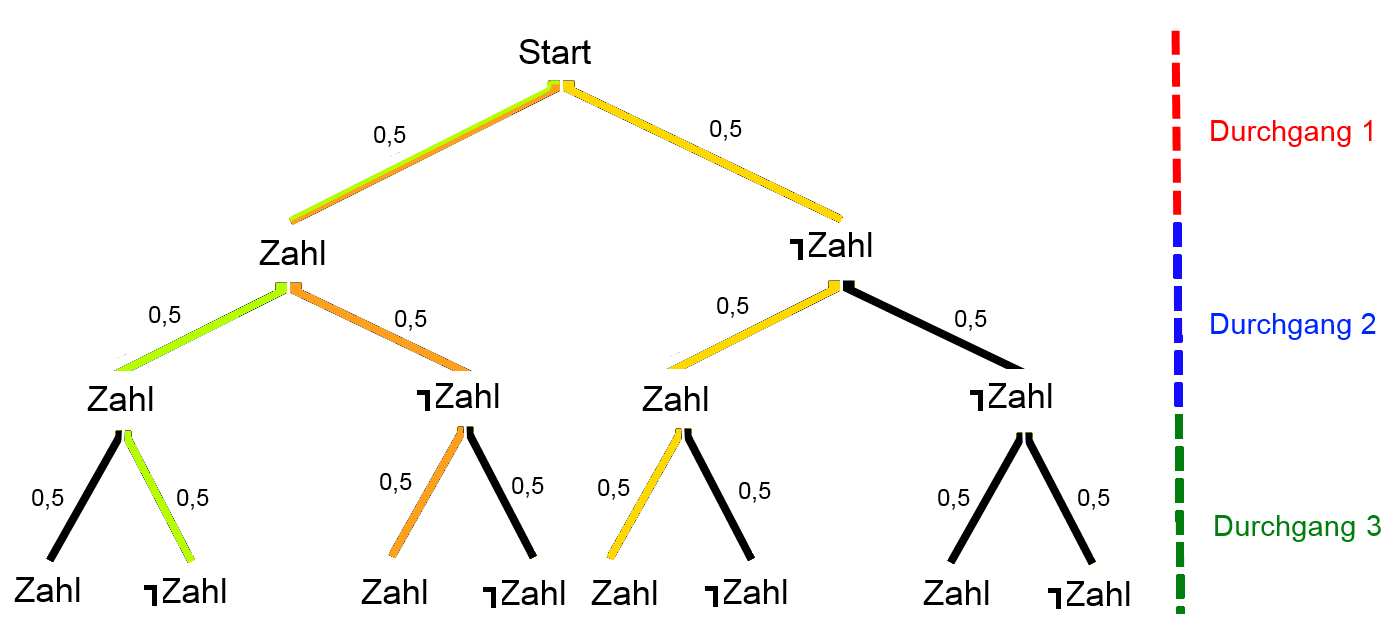
Die 3 verschiedenen Wege, das gewünschte Ergebnis zu bekommen sind hier bunt markiert.
Die Wahrscheinlichkeit setzt sich zusammen durch das Produkt der einzelnen Schritte · die Anzahl der Wege:
Produkt der Einzelnen Schritte: Zahl · Zahl · Kopf = 0,5 · 0,5 · 0,5 = 0,125
Es folgt:
P(zweimal Zahl und einmal Kopf) = Produkt der Schritte · Anzahl der Wege = 0,125 · 3 = 0,375
Macht man nun aber mehr als 3 Durchgänge, wirst du merken, dass die Wege und Möglichkeiten sehr schnell ansteigen und nicht mehr übersichtlich sind.
Zum Glück gibt es wieder eine Gleichung, in die wir nur noch einsetzen müssen:
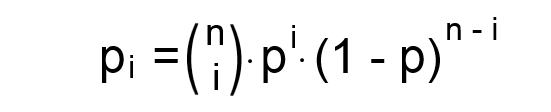
Diese sagt uns die Wahrscheinlichkeit von i Erfolgen bei n Durchgängen zu einer jeweiligen Wahrscheinlichkeit p.
Beispiel Münzwurf:
Wie wahrscheinlich ist es bei 5maligem werfen 3 Mal Zahl zu werfen?
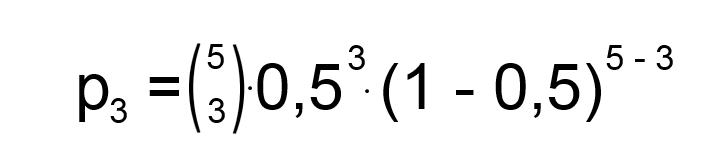
Doch nicht nur diese Gleichung bietet einen Einfachen Umgang mit der Binomialverteilung. Auch der Erwartungswert lässt sich viel leichter berechnen:
E = n · p
Beispiel: Die Wahrscheinlichkeit bei einem Würfel 6 zu werfen ist p = 1/6. Wie groß ist der Erwartungswert, wenn 12 mal gewürfelt wird?
E = 12 · 1/6 = 2
Das heißt wir erwarten, dass bei 12 mal würfeln ungefähr 2 Mal ein 6er gewürfelt wird.
Weitere Vorteile der Binomialverteilung sind die einfachen Berechnungen von Varianz und Standardabweichung:
Var(x) = n · p · (1 - p)
Die Standardabweichnung Sigma = σ ist wieder die Wurzel aus der Varianz.
|
|
4.6 Ende
|

 
|
Nun sind wir hier am Ende des Lernpfads angelangt.
Ich hoffe dir hat der Lernpfad gefallen und dass er dir geholfen hat!
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



