|
1.1 Allgemeines
|

 

|
Übertrage die wichtigsten Informationen des folgenden Textes in dein Heft!
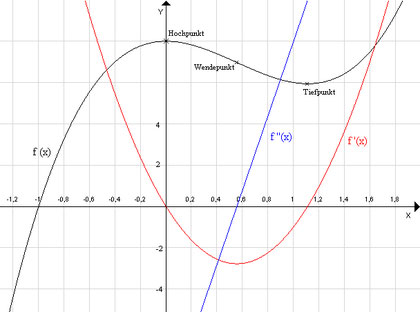
Bei einer sogenannten Kurvendiskussion geht es darum, mit wenig Aufwand im Wesentlichen den Verlauf des Graphen einer Funktion zu erkennen. Das Zeichnen eines Graphen aus einer Wertetabelle mit zufälligen Wertepaaren kann bei vielen Funktionen zu falschen Einschätzungen führen. Wertvolle Hilfe kann hier die Differentialrechnung bieten, mit deren Hilfe charakteristische Punkte des Graphen wie Hoch- und Tiefpunkte oder Wendepunkte gefunden werden können. Dabei ist es günstig, gefundene Ergebnisse sofort in ein Koordinatensystem einzutragen und so den Graphen der Funktion schrittweise zu zeichnen. Oft kann man im Verlauf der Kurvendiskussion aus vorliegenden Zwischenergebnissen schon weitere Fragen beantworten. Bei Bedarf können noch zusätzliche Funktionswerte berechnet werden.
Bei einer Kurvendiskussion kann man sich von der Behandlung folgender Punkte leiten lassen:
- Größtmöglicher Definitionsbereich, Stetigkeit, Polstellen
- Symmetrie
- Nullstellen
- Verhalten im Unendlichen, Asymptoten
- Extrema und Wendepunkte
- Graph zeichnen
Lernstoff
|
Lernpfadseite als User öffnen (Login)
Falls Sie noch kein registrierter User sind, können Sie sich einen neuen Zugang anlegen. Als registrierter User können Sie ein persönliches Lerntagebuch zu diesem Lernpfad anlegen.
|



